Physics of Sound: The Spectrogram (or what the heck am I looking at part 2)

I probably should give a little lesson on how to read a spectrogram, since my next post will feature spectrograms rather heavily.  I made all these spectrograms on PRAAT, which is free and downloadable if you wish to play with it.  (I know the website looks a little sketch, but I had to get it for my classes using the site I linked to and it's totally safe for your computer.)  PRAAT is a lovely piece of software that will record a sound and then give you both a spectrogram and a waveform of that sound.  As you look at the images below, the waveform is the image on the top with the thick black band and blue vertical lines, and the spectrogram is the grey-scale mess below that waveform.  So, on to the important part of this post!

How to read a spectrogram:

The x-axis (horizontal) is time, the y-axis (vertical) is frequency, and the grey-scale shows amplitude.  So a spectrogram can show three dimensions, time, frequency, and amplitude vs. a waveform that shows only two, time and frequency.  On fancier programs, the amplitude is sometimes shown in color, like having blue be the softest sounds and red being the loudest, but in PRAAT, the darker the band, the higher the amplitude.  In terms of the frequencies, I set the spectrograms to show from 0 Hz to 7000 Hz.  PRAAT can display up to 20,000 Hz, but then the formant bands I want to focus on get too squished together.  If you click and make the image bigger, you can see a dotted red line with a frequency number off to the left.  I set those lines there just to give you some idea of where the upper formant lies in terms of Hz.  And remember from the last post that the formant will be somewhere around this frequency, not right at the single frequency itself.

So this is what a typical spectrogram will look like with the upper frequency set at 7000 Hz.  (I think PRAAT's default setting is usually 5000 Hz.):

The spectrogram above is me sustaining the vowel /a/ with my speaking voice.  You can clearly see five dark bands going horizontally across the image, but the bottom two dark bands are the darkest, indicating that those are the highest amplitude formants.

Sustained-speech of an /a/ vowel with formants marked.

This is the same spectrogram as the one above it, but I've set PRAAT to show me the first five formants, which it does by adding in those red lines.  The software is simply determining where the highest amplitudes are and sticking bands in there.  I'm not controlling where those thick red lines go.

Sustained, spoken /i/ vowel, no formants marked in.

Here's me sustaining an /i/ vowel with my speaking voice.  Note the wide distance between the first and second formants, which is just what the /i/ vowel does.  Oh /i/, you so crazy!

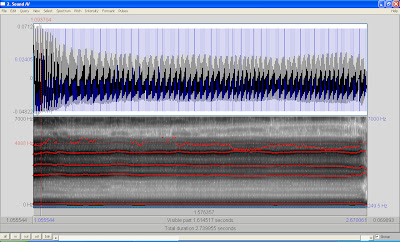Sustained, spoken /i/ vowel, first five formants marked in red.

Above is the same spectrogram again, but with PRAAT marking the first five formants in red.

Spoken phrase:  "One, two, three, go," no formants marked.

 And there's a spectrogram of me speaking the phrase, "one, two, three, go.'  Here, you can see the movement of the formants as I go through those words and the "white space" between the words.  (Those areas where there's a thick blue vertical band on the waveform is where the /t/ and the "th" sound of "two" and "three" are.  And, you can see the antiformants present in the /n/ sound right at the end of the first word "one."  Pretty cool, huh?)  (Scroll to the bottom of page 2 on that antiformant link to read more about them.) And here's the same phrase with the formants marked in:

"One, two, three, go," with formants marked in red.

Now, some super cool people can actually read spectrograms like they're reading words off the page.  I'm not quite that awesome yet, but if you tell me what the phrase is, I can pick out where each specific word is using my knowledge of vowel formants and consonant frequencies.  It'd be cool to become that person who can just read them, though!

Now the reason I kept setting the spectrogram to 7000 Hz instead of 5000 is two-fold:  First, I wanted to make sure the upper formant wasn't cut off since that formant does occasionally go higher than 5000 Hz, and second, I wanted you to see that there actually is a thick band of amplitude above the 5000 Hz mark, which you can see in the spectrogram above.  So there are more "formants" above that 5000 Hz mark...we just don't really regard frequencies higher than 5000 when discussing speech or singing very much.  (Although, this article does!)  Heck, PRAAT doesn't even mark in any formants above the 5000 Hz area...usually the fifth formant area.  But, I wanted to make sure you know that it's not like formants and harmonics just disappear above 5000 Hz.  Mathematically speaking, harmonics would just keep on going higher and higher, and so would formants.  However, the amplitude lessens the higher you go, so vocal harmonics and formants do dampen out eventually...just not at 5000 Hz.

Up next:  The singer's formant!  I'mma gonna break apart a common misconception in the hopes that it clarifies what is we're actually doing when we carry over that orchestra.

Physics of Sound Series: Formants, formants, and more formants

According to Raphael et al., the source-filter theory of speech production states that the source of vocal sound, i.e. the vocal folds, is filtered through the air spaces in the vocal tract (p. 330).*  This is a fairly simplistic model of vocal production, but it is very useful just because of its simplicity.  Other models of speech production out there get a lot more detailed, but for a general, conceptual knowledge of the relationship between the vocal folds and vocal tract in terms of acoustic output, I think the the source-filter model can't really be beat.

So what does this have to do with formants?  Well, on the last physics post, I left off by stating that the vocal tract can change it's shape and configuration to filter out different harmonics from the same sound source.  The shape of the vocal tract will also amplify certain harmonic frequencies, while dampening others.  The resulting "peaks" in amplitude at specific frequency ranges are what we call formants.  One important thing to note here is that formants are not the same thing as harmonics.  You can think of formants as being a certain specific collection of harmonics, so the first formant is not the same as the first harmonic.  The idea of a harmonic is that it is one particular sine wave that is related, mathematically, to the fundamental, but the formants are collections of these sine waves.  The language you typically see is that the first formant is around a specific frequency.  So while you might read about the singer's formant being somewhere around 3000 Hz, the formant isn't actually only at 3000 Hz, it's just a collection of frequencies centered somewhere around 3000 Hz.  I think the semantics might get a little fuzzy there for a lot of people, but what seems like a little, unimportant detail actually makes a big difference when discussing harmonics vs. formants.  If you use those terms interchangeably, you'll just confuse the folks who know they're different things and then you'll get confused that they're confused and yadda yadda yadda...

Think of it like this:  Let's say you have a collection of all the Star Trek episodes from every Star Trek series, even the crappy ones.  If you consider the first series, the original Star Trek, as the fundamental, the first "harmonic" would then be Star Trek:  The Next Generation, the second would be Deep Space Nine, the third Voyager, etc.  However, it's possible that if these "harmonics" get filtered into formants, the first formant could consist of the first five seasons of The Next Generation, with the last two seasons filtered down to really low amplitude.  The second formant could be the last four seasons of Deep Space Nine, with the first three seasons of DS9 being filtered down.  The third formant could be the last five seasons of Voyager with the first two seasons filtered down, etc.  See the difference?  So harmonics are the building blocks of formants, but harmonics come from the resonance of the vocal folds themselves and formants come from the resonance of the acoustic filter or vocal tract.

What's great about formants is that they happen to be the way we distinguish vowels during speech.  In fact, the relationship between vocal tract shape and the acoustic output (vocal sound once it exits the mouth) is so interrelated, we are able to classify vowels by both the vocal tract shape and the acoustic output, depending on what we're talking about.  I.e.:  Talking about articulation?  You'll be talking about the shape of the vocal tract made by the articulators (tongue, soft palate, etc.).

If you happened to click over to that Wikipedia article on vowels, you probably noticed there's a section on articulation and a separate section on acoustics.  The position of the tongue in the mouth happens to make the biggest difference to the overall shape of the vocal tract, and so, a lot of vowels can be categorized by place of tongue articulation during production.  For example:  An /i/ ("ee") vowel is categorized as a high, front vowel because the tongue is positioned very high near the roof of the mouth, but it is also positioned quite forward in the mouth and is, therefore, a high-front vowel.  A high-back vowel, such as /u/, has the tongue positioned as a "hump" near the back of the mouth, so it's high, but in the back.  A low vowel, such as /a/, doesn't involve the tongue in a raised position at all, and is closer to a neutral vowel position, of which the schwa sound is considered the most neutral.  (I know a lot of singers consider /a/ as the most neutral vowel, but linguists and speech scientists have researched tongue positions, and schwa is indeed the most neutral.  I think the reason singers like the focus on /a/ so much more is that we don't tend to sing schwa very often, and if we do, we don't sustain a sound on schwa.  So schwa gets kinda a bad-rap in the singing world, but it is an important little vowel in spoken language.)  

Because a larger space will resonant at lower frequencies, and a smaller one at higher frequencies, the formants are a result of the size of the pharyngeal space and/or oral space as determined by the tongue position, primarily.  A good example of this is if you tap on a glass with some water in it, then tap again after drinking the water, the second tap will be a lower pitch than the first tap because there is more air inside the glass after the water is gone to resonant the sound.  Or a better example:  A cello is bigger than a violin.  So...there you go.  Therefore, in a simplified sense, these tongue positions all correspond to the formant frequencies of each vowel.  The /i/ vowel is known for having a low first formant (more pharyngeal space created by the high tongue position) and a high second formant (small oral space created by tongue position,) and in fact, this vowel has the widest space between the first and second formant as it's trademark sound.  The /u/ vowel has a low first formant (from the high tongue position creating more pharyngeal space), but also has a low second formant (from the tongue position being near the back of the mouth, creating more space in the oral cavity).  Once again, this is a very simplified way of looking at this, but it's an easy way to understand the basic idea.  Just be aware that the science of acoustics can get pretty darn complicated in this area.


*Raphel, L. J., Borden, G. J., Harris, K. S. (2007).  Speech science primer:  Physiology, acoustics, perception of speech (5th ed.).  Philadelphia, PA:  Lippincott Williams & Williams.

The power of kindness

I keep a regular yoga practice.  I mainly practice at home, since it's free to do there, but I also attend yoga classes regularly at a good studio.  I tend to do yoga about two to three times a week.  However, this past spring semester, I ended up only practicing once a week, at most.  So, I got decently out of shape from what I'm used to and I ended up hurting my left hamstring, somehow.  What sucked the most about this was that my left leg has always been more flexible than my right leg, while my right leg tends to be stronger, so I was usually able to do hand-to-foot pose and this one-legged arm balance with my left leg pretty easily, while I still struggled a little with the right.  However, this summer, while I've been trying to nurse my left hamstring back to health, my sides have reversed.  I'm still not able to do these poses, or others like them, with my left leg, but I've gotten them down with my right.

So just today, while I was practicing at home, I realized that I've been so careful with my left leg this past few months that I've actually let it become weak.  I've stopped trying to engage the muscles on that leg as much because of the injury.  Of course, this is not helping recovery at all, so today, I started forcing that leg to pull it's weight, and while my hamstring still isn't totally better, I actually got my full trikonasana on the left side back today and my hamstring feels better now than it has in a long time.  I'm sure the more I focus on working the muscles on my left leg, the better it will get, and I will be back to my normal yoga practice pretty soon.

This little experience with my hamstring really reminded me of my vocal recuperation, probably because I had a conversation with another singer dealing with their own voice disorder just this week.  See, the thing is, I was acting like my hamstring was still injured, even though it's been months since the actual injury.  My hamstring is quite likely healed up, it's just healed tighter than it was before.  Because of this tightness, I've been avoiding really using it in yoga, making modifications on the left side for any hamstring-intensive pose and just allowing my lunge on that side to kinda go out of form.  In essence, I was allowing my muscle to stay weak just because I was still acting like something was wrong with it well after it was healed up.  In an earlier post, I said I had a hard time learning to trust my voice after it was healed up, because I felt like my voice had betrayed me by being injured.  But I've talked to a few singers out there dealing with injury who have the added issue of still feeling like their voice is injured even after therapy is completed and they're given a full bill of vocal health by their team.  So they're still fighting with their voice and letting it do the wrong things because they still think it just doesn't "work right," even though it does.  It's a mind game, isn't it?

What these injuries really do to us is force insecurity upon us, so naturally, our reaction is to defeat the insecurity.  Attack it full on so that we can get past it as quickly as possible.  But when this tactic burns out, as it often does for many people out there, we start to retreat into the insecurity, allowing it to defeat us and beat us down until we give up.  This can lead to regret and perhaps even bitterness for so many of us, and maybe we find the fire to fight again and maybe we win, but what if we just changed our perspective of this insecurity?  What if, instead of fighting, we decide to accept this weakness that has been thrust upon us and still decide to be kind to ourselves?  And what if, by being kind to our whole new self, insecurity and weakness and all, we learn how to patiently and diligently work through our injury, not by forcing ourselves to be as we were before, but by moving toward being someone new and different because of this experience?  What if all we need to do is realize that healing doesn't typically mean going back to how things were before, but it can mean becoming better than we were before?

I suppose saying I'll get back to my normal yoga practice is a bit of a lie, because before this injury, my right side was more inflexible than it is now.  If my left side is restored to it's former, flexible state, my whole body will actually be more balanced than it was before this.  Just like how, even if my voice is only better because of being healed and the glories of vocal technique, I'm a better, more joyful singer because there was a time when singing was taken away from me.  So to all those out there recuperating from any injury:  May recovery make us all stronger, more balanced, and more joyful; may we be kind to ourselves and patient with our injury as we build our strength back up; and may we all realize that we will never be the same...and that can certainly be a good thing.

Why yes I DO like school, thank you very much

There's a common statement I tend to hear from certain people when they find out that yes, I am going back to school for yet another graduate degree:  "You must like school."  This statement is always delivered with a bit of snark and a slight roll of the eye, and it is usually said by people who say they were "never good at the whole school thing."  That phrase is almost always followed up with the person explaining how great their (insert job title with major company) is and that they get paid (insert regular hourly wage/typical management salary) and they never needed a degree to do it.  The rather clear subtext to this exchange is thus:  "You poor, nerdy sap.  You must be in school because you're avoiding the real world.  You should suck it up and just get a job like everyone else."

What I find the most interesting about these exchanges are the implicit assumptions that are made about people who seek additional degrees at all.  The main assumption tends to be that anyone who gets a degree higher than a bachelor's or a second bachelor's is a "career student;" you know, someone who's just avoiding adult responsibility by staying in school as long as possible.  I find this assumption interesting in light of two facts:  The fact that I have been out of school for several years now and have been an independent adult through all of those years, and the fact that there are a lot of health/medical professions that require a graduate degree for licensure.  I know I can't expect the general populace to know what requirements there are for certain professions, but why do some of these folks not drop the snark when I tell them that?  Why not just trust that those degrees are required because there is a vast body of knowledge and many hours of training required to do the job effectively?  People trust MDs are valid professional graduate degrees, so why not trust that physical therapists, occupational therapists, physicians assistants, audiologists, speech-language pathologists, etc., need advanced knowledge to effectively do their job?

But it's the implicit insult that really gets me:  "Nerd."  Now, I know that in today's society, the term "nerd" has been usurped to mean anyone who's really, really into pretty much anything and is not really seen as an insult anymore, but in this setting, it's intended as one.  Perhaps there are just too many grad students out there who are intellectual snobs.  Maybe these folks have encountered so many of those snobs that they get all defensive and mistakenly think someone with multiple degrees is automatically a snob.  I can definitely sense a bit of insecurity from the other person in this exchange.  Maybe they always wanted more out of life, but gave up on their dreams.  Maybe they always struggled in school and felt inferior to a sibling or friend who always found school easy.  Maybe they did well in school, but only because of a near-abusive "tiger mom," and so they hated school as much as they were good at it.  As much as I believe insecurity is nothing to be ashamed of, I also believe personal insecurity is never a valid excuse for making another person feel like crap.  I believe this as much as I believe that salaries and job titles do not define the intrinsic worth of another human being.

My reactions to these situations have never been the best.  I usually end up explaining the good employment prospects and the typical starting salaries in the field, but this is in stark contrast to the belief I just stated above, isn't it?  So I end up feeling put down, but also a little dirty for defending my life decisions based on their criteria of self-worth.  The thing is, that is not my criteria.

So, after having one too many of these situations in the past, I have decided to arm myself with a response I can feel good about (which will be truncated in real life):
Why yes, I do like school.  I like to learn.  I enjoy broadening my mind and discovering new and exciting things that I never knew about before.  I like the idea of helping forward the advancement of society and human knowledge through research.  I like the pragmatic side of this new field, where I get to help an individual who is struggling with a disorder that keeps them from effectively communicating.  I like school.  I like that it is not only an avenue through which I can pursue my dreams and sharpen my mind, but it is also a safe place to learn, try, discover, fail, try again, and, ultimately, succeed.  I like learning, and I like that I will continue to learn, grow, and develop throughout my life thanks to the mental training higher education has given me.  With all the people in the world who use knowledge and education to keep others down, I like that I am becoming someone who will counter those greedy individuals, and who will use her knowledge and education to help others in need of it.  I think education provides me with a value beyond just a salary and job title.  It provides me with a sense of purpose and direction and the ability to accomplish my goals.  Isn't that ultimately what we are all searching for?

Physics of Sound Series: Harmonics and fixed strings and open-closed tubes, oh my!

So, we've got the vocal folds acting like a fixed string with multiple resonant frequencies called harmonics, but before we go further, I realized there was some terminology that I should go over.  Remember how the actual sound wave produced from vocal fold vibration is far more complicated than that of a single string?  That's mainly due to the motion of the lamina propria, but even single strings can produce complex sound waves.  This is a wave pattern that is created from the interaction of multiple frequencies known as harmonics.  If you have several, or even thousands, of simple sine waves that are harmonically related, you've got a complex periodic sound wave.  Periodic means it still has a predictable pattern, as opposed to complex aperiodic waves, like white noise.  But the linguistic signal contains both periodic and aperiodic waves.  Periodic would be vocal sounds, like vowels; aperiodic would be like unvoiced consonants like /s/, and a combination of periodic and aperiodic happens during a lot of voiced consonants, like /z/.  We're just going to focus on complex periodic waves for the purposes of understanding resonance more fully.  Complex periodic waves can be broken down into their simple sine wave components by using something called a Fourier transform.  We certainly won't go through the math for all of that, but just know that all complex periodic waves are made up of simple sine waves, and even though the vocal folds create a more complicated sound than a string does, we're going to continue with the string comparison cause I think it makes everything so much easier to visualize.


The thing about vibrating strings fixed at both ends is that they have a fundamental resonance of 2 times the length of the string.  This just means that one-half of a wave can "fit" on a string at any given pass along the string.  It also means that the string will vibrate at both even and odd harmonics of the fundamental.  This can be represented mathematically if we use our knowledge of frequency = velocity divided by wavelength.  In this basic case, we're going to consider velocity to be the speed of the wave being produced, and in the human voice, that speed is determined by the tension and mass of the vocal folds.  So when the folds elongate, tension increases and mass decreases resulting in a high frequency of vibration (cool, huh?).  And the wavelength, thanks to the half-wave resonator we're working with here, will be two times the length of the string (or folds).  Using this equation and setting our speed at 340 meters per second, the approximate speed of sound at sea level, we can figure out the harmonics of a 1 meter string.  The fundamental frequency would be 170 Hz, the first harmonic would be 340 Hz, the second harmonic would be 510 Hz, the third 680 Hz, the fourth at 850 Hz etc.  This sound wave (up to the fourth harmonic) would sound like this:

Record music with Vocaroo >>
File made with Audacity

Now that we've compared the vocal folds to strings, what do we have to compare the vocal tract to?  An open-closed tube!  ...which is not that exciting at all.  But what the vocal tract does is pretty darn exciting.  Of course, the vocal tract itself can change it's shape for communication and such, but the open-closed tube is a good simplification of what the basic function of the vocal tract is.  An open-closed tube is a quarter-wave resonator, as opposed to the half-wave resonator that the string up there is.  So what does that mean?  A quarter-wave resonator means that only a quarter of the wave can "fit" during one pass through the tube.  So this resonator only vibrates at odd harmonics of the fundamental frequency.  So, if we look at that 170 Hz frequency produced from that meter-long string up there, The open-closed tube resonating at this fundamental 170 Hz would have a length of 0.5 meters and the first harmonic would be at 510 Hz, the second at 850 Hz, etc.  Notice something there?  This tube is only resonating at even frequencies of the string up there.  So what happens to the sound wave produced by that string as it passes through this tube?  Well, it'll sound something like this:

Record and upload voice >>

File made with Audacity

Where did those other harmonics go?  The tube ate them.  No really!  Well...it kinda-sorta did.  See, the tube acts as a filter for that sound wave.  Those missing frequencies, the ones that the tube won't resonate, are going to be filtered out due to destructive interference, while the frequencies the tube vibrates at are going to constructively interfere and exit the tube for us to hear.  Yup, that's right.  Without resonance, we wouldn't hear our own speech, much less a singer singing over an orchestra.  Your voice is always resonating all of the time; it's just that opera singing requires a difference resonance than your speaking voice...obviously.  We don't really sound like we're talking when we're singing, do we?  

Now, I don't know about you, but I personally find the second audio file a little more pleasing than the first.  The first one is objectively "richer," in the sense that it has more harmonics, but the second one subjectively sounds "richer" to me.  I'm not really sure why, but I suspect it has something to do with the fact that I am physiology wired to find the sound of the human voice important, as are you, and so perhaps I also find sounds from an open-closed tube more pleasing?  (And if you didn't find this to be true, you're really messed up!  Just kidding.)  And where this "pleasing" association would occur in the brain, I'm not sure.  But I know my brain is associating the second file with a richer sound that I happen to find more pleasing, because the first sound has more harmonics in it for sure...I would know; I inputted the frequencies myself!  But if you played those two tones for me without my knowing about the harmonic structure, I would assume the second one has more harmonics.  The brain sure is one crazy organ, amirite?  Of course, I digress, but this is an example of some of the stuff people are trying to figure out in terms of how we listen, pick out, and associate the speech signal into meaning in our lives all day long.  It's some cool stuff, for sure.  Perhaps I'll learn an answer to that soon and will update you guys.

Now, in a stationary tube, the harmonics are pretty fixed, but lucky for us, our vocal tract can change shape, length and configuration to produce a lot of different sounds.  By changing it's shape, the vocal tract filters the same sound source differently, producing all of the different sounds we make in our languages and then some.  Conveniently for us, it seems to do this pretty much on auto-pilot most of the time, like when we're speaking, or how the vocal tract lengthens when our voice drops in pitch (the larger cavity will resonant at lower frequencies and shorter at higher).  The shape the tract takes determines which frequencies are amplified and which ones are dampened out.  And this sets us up quite nicely to talk about formants next time, doesn't it?

Resources: 

http://www.physicsclassroom.com/

Raphel, L. J., Borden, G. J., Harris, K. S. (2007).  Speech science primer:  Physiology, acoustics, perception of speech (5th ed.).  Philadelphia, PA:  Lippincott Williams & Williams.

The balance between the rift

There's a funny thing that happens when you learn a lot of valuable information in a short amount of time.  You tend to forget that not everyone is having the same experience you are.  I think this is even more pronounced in people who tend to be rather ambitious, like me.  I know that in society in general, ambitious people are lauded, but there's a distinction between an ambitious person who has reached a level of success and an ambitious person who is just starting out.  The successful person is seen as someone to look up to, and the new student to a discipline is seen as, well, a n00b.

We n00b's, by my definition, tend to be a bit crazy, you see.  We geek out to anyone who shows even a tiny bit of interest in what we do.  We find ourselves talking far too long about some nuance of our discipline without realizing it.  In short, we are awkward and alienating.  We're like someone who's just fallen in love, and we just can't help ourselves.  However, we usually know we are a little different than others.  I think I get it from my father.  I once said Dad is a guy who doesn't have "hobbies" he has "obsessions," and, while I do have a few hobbies, I will say that voice science has become an obsession.  I can only hope that my cohort of master's students won't mind, and perhaps they will even be the same.

I was like this with opera too, and really, I still am if given the chance.  But the years have taught me that very few people can tolerate a singer geeking out about opera for too long before they politely excuse themselves.  SLP is a little different, if only because if someone knows what it is, they usually either know someone who went to one, or they went to one themselves.  Therefore, they seem to appreciate learning a little more about this profession, usually from the respect they feel toward that SLP who gave their parent a swallow evaluation at the hospital, treated their autistic child, or helped their grandparent after their stroke.  For opera singers, though, we're just seen as a novelty, and people don't usually treat you with the same level of respect, perhaps because they've either never been to an opera or have never met an opera singer before.  (Or worse yet, perhaps they have and that is why they don't respect them.  Parish the thought!)  This always ruffles my feathers, because I still strongly feel that, while the value in opera is subjective, it still has value nonetheless.  And really, what kind of person are you if you don't at least respect someone for their craft even if you don't see the value in it?  (But perhaps the issue lies in the general public not knowing about the craft itself and the training it requires...but I digress.)

What's interesting to me is that while I seem to have gained some respect and/or interest from random people I meet, I've lost a bit with (some) singers, particularly the ones who didn't know me before.  Maybe it's that whole "abandoning" the musical profession thing, but I can certainly see that I've become an outsider.  You know, someone who no longer understands the demands of the profession, or appreciates what the real professional singers go through.  The biggest issue I have with this is I find myself wanting to abandon the singing world altogether.  Why go into voice research?  Why be interested in treating voice professionals when I get out?  They're just going to treat me like I don't understand them anyway.  I know this is really just an immature reaction from me generalizing a small portion of the singing population, but I find myself heartbroken all the same.  Opera was my first love, profession-wise.  I'll never really leave it.  I may not train as hard as I used to when I was auditioning, mainly because I no longer have the time, but I still sing.  I still remember the training from my master's program and beyond.  I know I've gotten a bit rusty, but I can still run the race, even if I can't run it in the Olympics.  (Course, I never got a great deal of respect from singers when I was in the profession either, but that's another story...one that I don't really need to write.)

All my new knowledge I've gained in voice science, and it's been significantly more than my pedagogy program, helped me a great deal.  I was able to train smarter and more efficiently as a singer and I became a more efficient teacher.  I noticed I was able to help my students with a vocal problem within weeks instead of months and months instead of years.  I was a good teacher before, but I'm a better teacher now.  But, I've gain new, more specific terminology that makes it harder to communicate with other voice teachers.  I can see a rift forming in my mind just as it is forming in those singers who see me as an outsider.

That rift is the burden of knowledge.  I know that sounds pompous, but it really isn't.  On the contrary, it is a lonely place.  It is the divide that comes when you forget exactly how much your target audience knows and how much they don't know.  If you assume they know more than they do, you talk over their heads and seem like a pompous blow-hard who just wants to show them up intellectually.  Assume they know less, and you seem condescending.  As I integrate new knowledge, it solidifies, and I forget what it is I didn't know two years ago.  Everything I've gained is just elementary stuff to the professors and licenced SLPs in my new field, and as such, I approach a lot of this as if it is elementary.  However, some of this stuff is way beyond what some singers learn in pedagogy courses, so forgetting that makes the rift larger.  And yet for others it is not all that far off; it really just depends on the school.  So how does one begin to talk about it without falling into that rift?  Maybe I'll never learn to find the balance.  To talk in a way that doesn't alienate or deride and to be seen as a colleague to singers instead of a traitor and offender.  And maybe I'll never stop being an outsider.  I hope I find that balance someday, though, cause I would rather be of help to others (who wish for it) than to drift away in the rift.

One journey ends, another begins

Well, what the heck have I been up to!  It's been a really long time since I posted last, huh?  Where did I disappear to?  Answer:  School.  Last semester literally sucked up all the time I had.  Long story short:  I was taking all non-SLP related courses that left me a bit burnt out.  Sorry I disappeared like that, though!

Sometimes, I hear from singers thinking about getting into SLP themselves.  I usually tell them to prepare for a time-intensive, difficult journey, but I realized that the difficulty is one area of my journey I had kind of been avoiding on here.  So, truth time.  This post is all about that point from deciding to be an SLP to the point of beginning graduate school in it, which for me, will be this August.

My journey to being a speech pathologist hasn't been a smooth one.  I'm actually just going to be starting my master's program this coming year.  Which, if you've been counting, means I've been taking undergraduate courses for two years now just to get to the point where I could do the two-year master's program.  I honestly did not expect it to take this long.

Rewind to fall of 2010.  I decided to become an SLP.  I applied to my local university, since they have a three-year program for non-SLP undergraduate majors.  I didn't get in, and that kinda sucked.  I mean, I had finally gotten that fire-in-the-belly feeling about my life direction, so not getting in felt like just another failure on top of all the music-world failures I had accumulated over the years.  Ain't that how it goes, though?  You feel like life is getting back "on track" after a set-back and, low and behold, there's another set-back waiting right around the corner.  I didn't want to wait any longer!  I wanted momentum in my life!  I wanted direction...but I got rejection.  Good times.

See, I knew I had at least one year of undergraduate courses I would need to complete before I could start a clinical program.  That's just how it goes for folks who weren't SLP undergraduates, but the day after the rejection letter came, the school told me their "leveling" program (as it's called) was full already.  Luckily, they also informed me there was another leveling program at a state school in *big city* nearby.  I applied to the state school's program right away, and I was registered for fall classes by the end of the week.  Whew!  Momentum was back, and I was on my way!  *happy dance*

During that fall semester, I applied to about six graduate schools across the nation.  My then-fiance and I tried to line up our schools, since he was going to graduate school in a STEM field.  We played the waiting game, and it turned out that I got into one program out of the six.  (Turns out, SLP is kinda hot right now just cause there are still jobs in that field, so schools are getting waaaaayy more applicants than it used to, but slots are still quite limited.  Therefore, getting into grad school has become quite the challenge to many of us levelers out there.)  However, our problem was that the program wasn't in a city where he got admitted.  In addition to that, the cost of that particular program was ridiculous!  About two-thirds more than most SLP programs, and the city where it was located is one of the most expensive to live in.  Meanwhile, my SO got admitted with full funding and a stipend to a top-ten program in his field, which also happened to be in a town with a low cost of living.  So, I turned down the one crazy-expensive program and we headed out to where he was going to school.

I took a gamble on new plan:  Take some science and math courses, which I would need eventually for my licence anyway, and apply to the two programs in our new state.  I reviewed math, with the help of my now-husband, and passed my way into Calculus I, and I also took a psychology course that fall I would need later.  This past spring semester, I took Calculus II, Introduction to Mechanics (which what calculus-based Physics I is called here), and another psychology course online.  Do SLPs need calculus and calc-based physics?  No.  But I took them because during my leveling program, I starting thinking I would actually continue to get my PhD after my master's degree, and strong math/physics knowledge would help in one of my research interests immensely.  (I'm kinda an over-achiever like that.  And besides, I also figured taking some classes beyond what most SLP undergrads take would set me apart, so I figured it was a win-win...as long as I got good grades.)

And luckily, my gamble paid off!  I got into both schools!  Yay!  *Big happy dance*  So now, here I sit.  Waiting to actually begin my journey of becoming an SLP.  Well, I suppose that's not entirely true, since I've spent two years studying to get here, but I sorta feels true.  It's been a much longer journey just to begin the privilege of clinical training than I ever thought it would be.  If this journey was shown in some movie-montage, it would be probably be a very boring montage; mostly consisting of me sitting and studying at a coffee shop, at home, and at school.  (Huh...I guess there's a good reason Hollywood has stayed away from the study-themed montage.)  If I had known it would take this long would I have done it?  I'm honestly not sure, but now that I've learned what I've learned so far, I'm glad I did it.  If I have one talent and passion for any one thing it's learning.  (I. am. a. geek.)

I'm sitting here with aspirations of greatness...not too unlike my 18-year-old singer-self back in undergraduate days.  The only difference is, my 18-year-old self was doing her best not to be crippled by the fear of failure, but my thirty-something self has no such fear.  Not because failure couldn't happen, I know enough of probability to never say never, but because experience as taught me that failure really isn't something to fear.  I know, I know, could I be more cliche?  Here's the distinction I really want to draw for you, though:  Not fearing failure isn't the same as inviting failure.  I'd be quite content if failure never showed up ever again and I'm going to plan my ass off and work my ass off to keep it at bay.  But by not fearing it, I can look at any challenge square in the face and say, "Bring it.  Cause I'm all in."  Cliche?  Yes.  Freeing?  Absolutely!

The Physics of Sound: Resonance and Standing Waves

So what does happen when two sound waves are in phase with one another?  The two waves constructively interfere with one another to result in one wave that this double the amplitude of the two waves.  Basically, they both add up like some awesome crime-fighting team...and they...help people hear and stuff.  (Yeah...I don't know where I was going with that metaphor.)  Anyway, to better understand this, let's talk a little more about the phenomenon of interference.

Interference is when two waves sorta "line up" together.  Depending on how they "line up," the two waves combine to form one wave that is either of lesser or greater amplitude than the two waves were just on their own.  Think of it like this:  If one wave is going along with an amplitude of, let's say, 2 dB, and it meets up with another wave that's out of phase with this first wave, and the second wave's amplitude is 1.5 dB, then the resultant effect will be the 1.5 dB wave "canceling out" some of the amplitude of the first wave.  So you'd get a net result of a 0.5 dB sound wave.  If, however, the 2 dB sound wave meets up with a wave that's totally in phase with it, and this wave is going along at 2 dB, the resultant wave will be 4 dB.  So, yes, interference is very much like when you hang out with that soul-sucking person you really shouldn't be around (destructive) or that person who just makes you feel great (constructive).  (That's a super-basic way to represent interference mathematically, and the real math is much, much more detailed and complex, but it's just there to give you an idea.  So please don't go around thinking it's just addition and subtraction when scientists are figuring out interference.  It'd be a bit like those people who think a graduate degree in vocal performance just means you sing karaoke all day and get a degree for it.)

Sound waves travel along just fine until they hit a boundary.  When that happens, the waves bounce off the boundary and become reflected waves.  The initial wave, called the incident wave, can meet up with the reflected wave where the two waves interfere with one another to form a new wave that is the sum of the other two waves.  This is called the principle of superposition.  (I know I'm getting a bit redundant, but hang with me here.)  If, during superposition, two waves meet up that are completely in phase, the result is a standing wave.

As you can see above, one type of standing wave doesn't travel anywhere.  It stays in the same place constantly.  This results in areas where the displacement is zero, called nodes (shown by the red dots above), and areas of maximum displacement called antinodes (the tall peaks and valleys above).  So the constructive interference of an initial wave meeting up with a reflective wave to form a standing wave looks something like this:

The red and blue waves meet up to form the standing wave in black.  Other cool animations can be found here and here. 

But how do standing waves that don't go anywhere contribute to a singer's resonance?  Well, that question is kinda jumping a bit farther ahead than where we are now.  For now, just think about standing waves on a medium that is fixed on both ends, like a string.  Ever played with a string or  necklace where you bounce the string up and down?  If you have, you actually formed a standing wave at the string's first resonant frequency, called the fundamental frequency.  But the string does have other frequencies it could resonant at, called overtones.

First fundamental and first six overtones of a string

But why am I talking about strings?  What do strings have to do with vocal resonance?  Think about it a second:  What acts like vibrating strings with fixed ends when we speak or sing?  Yup, the vocal folds.  But, the vocal folds vibrate in patterns that are much more complex than just a single string.  Remember how the air opens them from the bottom to the top, due to subglottal air pressure, and then the folds get sucked in laterally because of the Bernoulli effect?  The resulting wave pattern is very intricate,which results in a complex waveform (multiple simple sine waves going out at once) being produced at the level of the vocal folds.  The fundamental frequency and all of the overtones of the human voice originate at the level of the vocal folds.

*That last bit is very, very important, and it seems to be where a lot of singers get very confused...usually not due to any fault of their own.  The vocal tract absolutely cannot create sound waves or overtones to those sound waves:  Not the singer's formant, not the harmonics, not any of it.  All of the frequencies picked up by a spectrograph originate from vocal fold vibration.  The vocal tract only acts as a filter for the frequencies sent out by the vibrational pattern of the vocal folds.  And that's where we'll pick up next time!

Raphel, L. J., Borden, G. J., Harris, K. S. (2007).  Speech science primer:  Physiology, acoustics, perception of speech (5th ed.).  Philadelphia, PA:  Lippincott Williams & Williams.

Physics of Sound Series: The Waveform (or, What the Heck am I Looking At?)

We now know that a sound wave is made up of moments of compression and rarefaction, and we know a little bit about a waveform as well.  But there are other parts to a wave that we need to know about before we get into just what resonance really is.  Those parts are:  Period, frequency, amplitude, phase, and wavelength.

No doubt, you've heard of some of these before.  Frequency and amplitude, in particular, get a lot of attention in the music world.  A lot of times, we talk about frequency and amplitude as synonymous with pitch and loudness, and for most purposes they are.  However, when I talk about frequency and amplitude, I'm going to be referring to the actual physical properties of the sound wave (or waves), meaning the parts of the wave that can be measured with proper instrumentation and then studied.  Therefore, frequency and amplitude are objective measurements.  Pitch and loudness are usually associated with the perceptual properties of the wave, i.e. just how loud or how high/low a person perceives that sound differs from person to person (and from ear to ear, for that matter); so pitch and loudness cannot be measured per se, but rather discussed subjectively.  (And remember from my previous post:  Anytime I'm talking about perception, I'm talking about the interaction from a sensory signal with a person's higher cognitive functions and life experiences.  Therefore, perception is always subjective.)

Yup, those are the same sine and cosine functions from trigonometry that you see on your calculator.

When you look at the waveform of a basic sine wave (the red line) shown above, you'll see that it has a repeating pattern.  The number of repeats of this pattern in a given amount of time is called the frequency of the wave.  This is usually given in Hertz, but can also be stated as the number of cycles per second of the wave pattern.  (See, it was originally called cycles per second (cps), but then the International Electrotechnical Commission (IEC) decided to honor Heinrich Hertz's contribution to the field of electromagnetism, so they gave him a unit of measurement, cps, and called it Hertz (Hz).  Scientists are always re-naming units to honor the great contributors to the field.  Sorta like how medical terminology is also littered with the names of big anatomy contributors, etc.)  So, for the famous A440 that orchestra's (supposedly) tune to, the frequency is 440 cycles per second, or 440 Hz.  In math terms, frequency is shown by:  frequency = velocity over wavelength (f = v/λ).  Sounds pretty fancy, but the reason I'm putting this here is because the period of a wave is related to the frequency.  The period is how long it takes for one cycle of the wave pattern to complete itself.  So if the frequency could be shown as: 1/period, then the period is shown by:  1/frequency.  Seems like we're talking about the same thing, but in general, the frequency refers to how often the wave pattern is repeating itself where the period refers to how long it takes for one pattern of the wave to complete itself.  Why do we bother with this distinction?  Well, because it comes in really handy for mathematical analysis of wave patterns.  Why should singers bother to know about this?  Because...well...I'll get there for ya.  (Besides, if your ever playing around with PRAAT or some other spectrograph software, you'll probably see options for period or frequency change, and you might want to know what you're changing out as you play around.)

Wavelength corresponds to the distance one cycle of the wave travels.  Slower frequencies have longer wavelengths, so one cycle of A440 travels double the distance through the atmosphere than A880.  (In the above equations, wavelength is represented by that funny-looking symbol, which turns out to be the Greek letter lambda.  So now, when you poke around wikipedia and see frequency equations, you'll know some of what you're looking at.)

The amplitude of a wave corresponds to it's perceptual loudness, and is related to the amount of displacement the air particles go through in the sound wave.  Because it has to do with how far each particle is being "pushed," amplitude represents the atmospheric pressure of a sound wave, and is measured in decibels (dB).  In the waveform shown above, amplitude is represented on the vertical axis.  So if the sine wave had a higher amplitude, it would have taller peeks and lower valleys, going past the 1.00 marked above.  Even though amplitude of sound is represented by this vertical displacement on the waveform, in longitudinal waves, the displacement in the real world is happening horizontally.  This is different for other wave types, like light, but the math and the graphical representations are the same.  (I just want to point that out because it's easy to misinterpret the sound waves from your mouth as looking just like the waveform representation, but if we could see the sound wave, it would like more like the animation here.  That's kinda important to remember once we get to the anatomy of the ear and the role the ear drum plays in hearing.  And, oh yeah!  I'm going to get into the anatomy of the ear and how it plays a role in resonance as well, for both the audience and the singer!)

Phase is where we start to get into some important stuff when it comes to understanding resonance, and especially the phenomenon of standing waves.  The phase of the sine wave in the above picture basically is where in the cycle the wave starts when you're looking at the vertical axis.  Let's look at it more closely:

See how the sine wave is passing through the vertical axis where the horizontal line equals 0?  Now look at the cosine wave (blue, dotted line).  Cosine is passing through that vertical axis where a horizontal line equals 1.  So the phase of the sine wave is not the same as the phase of the cosine wave.  The fancy way of saying that is that cosine has a different phase shift than sine.  In fact, that's actually the main difference between sine and cosine:  The phase shift between the two.

Phase is really, really important because if you have two sound waves that are out-of-shift like this:

Look at the three middle waves to see the phase difference.

You'll see how when one wave has a peek in its amplitude, the other wave has a valley, or a negative amplitude.  This means that when one wave is in it's period of compression, the other is in rarefaction.  The result is that these two waves actually cancel each other out, because if the atmospheric pressure is equally positive in one wave while the pressure is equally negative from the other wave, the two pressure differences cancel each other out.  1-1=0, right?  Crazy, huh?

But what happens when two sound waves are perfectly in phase?  What if you've got 1 + 1 instead of 1 -1?  That's where the phenomenon of standing waves comes in, and that's what we'll start up with next time.  Stay tuned!

Raphel, L. J., Borden, G. J., Harris, K. S. (2007).  Speech science primer:  Physiology, acoustics, perception of speech (5th ed.).  Philadelphia, PA:  Lippincott Williams & Williams.

Physics of Sound Series: The Acoustic Wave

I always have the hardest time starting up these series, because I spend a lot of time trying to figure out where to start.  I always know what the ending conclusion should be, but what's the beginning?  What's basic without being too basic?  So I'm going to start out where I think it should start out, but if I'm not being basic enough, please feel free to post any questions you may have.

Everybody always talks about resonance in the singing world.  Resonance, resonance, resonance.  Let's face it, as opera singers, we're pretty obsessed about it.  And why wouldn't we be?  It is, after all, the key to how opera singing works.  It is exactly how we are able to sing over an orchestra for hours at a time without hurting our voices.  The only issue I have with all this resonance talk is that it is painfully obvious that (some) singers have absolutely no clue what resonance really is.  It often gets talked about as a subjective thing that changes from person to person.  This is understandable given that so much of the sensation of singing is subjective, and therefore, how we teach singing is subjective.  It only makes sense that singers would start to think everything about singing is subjective somehow.  However, when we take something from the hard sciences, like resonance, and think of it as something that acts differently from person to person, as if it doesn't follow the laws of nature, we kinda sound like fools.  The other issue with all this resonance-as-subjective talk is that it makes what could be very clear pedagogy very fuzzy and confusing.  So, in order to fully understand what resonance is and how it can help us sing better, let's start with how a single sound wave works.

There are a lot of things in nature that function like waves:  Light, sound, the water in your bathtub...(okay, fine, ocean water too), but what exactly does that mean for sound to have a wave-like pattern of behavior?  Well, here's the definition of a wave from physics:  "a disturbance (an oscillation) that travels through space and time, accompanied by a transfer of energy...often with no permanent displacement of the particles of the medium (Wikipedia)."  Sounds pretty fancy, am I right?  But it does make a lot of sense.  If you drop a rock straight down into a body of still water, the rock disturbs the water's stillness causing a rippling of waves that travel out to the edges of that body of water.  Energy was transferred from the rock to the water which then traveled out to the edges of the body of water.  The water itself, though, will return to being still, i.e. it doesn't just keep traveling away from the rock until there's no water left, so there wasn't a permanent displacement of the particles of that water (you know, H₂O).

So what's the "medium" for sound waves?  Air particles!  All the lovely little air particles that make up our atmosphere is the medium for all the sound waves we hear, and the ones we don't hear too (i.e. ultrasound, infrasound, etc).  For our purposes, we'll think of a sound wave as beginning with air particles at rest.  An external force then comes along and sets those particles in motion (like when the electric slide is played at a wedding...sorry, couldn't resist.)  Anyways, let's imagine those particles are all lined up nicely next to one another.  The particles in row A, the ones closest to the external force, then get "pushed" up towards the particles in row B.  This is where we say the row A particles are "compressed" against row B, which then gets pushed up against row C, and so on.  (Anyone who's ever seen elementary-school kids line up for recess knows what I'm talking about here.)  So while each row is going into it's period of compression with the particles in front of it, the rows that have already been compressed then go into a period of rarefaction.  This would be when row A, after compressing with row B, swings back towards it's resting position.  But instead of landing at rest, row A actually over-shoots its resting position and ends up being spaced out farther from the row B particles.  If we want to get even more specific here, the property of inertia for those particles causes row A to compress with row B, then the property of elasticity over-takes row A's inertia, sending the particles back towards resting.  However, the property of inertia for that row of particles then over-takes elasticity and causes row A to over-shoot it's resting position.  But, don't fear, cause elasticity will over-take inertia and send row A back to towards resting.  This process will repeat itself until row A is again completely at rest.  Sounds complicated, but if you've ever set a pendulum into motion and watched until it came to rest again, you've seen this same action at work.  (*Edit to add:  This pattern of motion is called simple harmonic motion and is actually what pretty much everything in nature can be reduced to.)

This pattern of compression and rarefaction makes up what we call the sound wave.  This is why sound waves are sometimes called compression waves, but more commonly, they are called longitudinal waves.  (If you clicked on the link I had above on "compressed," you probably saw that coming.)  I encourage you to go ahead over to the link for longitudinal waves, because there are some very nice animations over there for you to see these waves in action.

One last thing before I sign off:  This pattern of compression and rarefaction is often graphically represented as a waveform.  Typically, waveforms are set on a typical Cartesian coordinate system (the graphs with x and y from math class), with the y, or vertical, axis representing the amount of displacement, which also happens to be the amplitude of the sound wave, and the horizontal axis representing the amount of time the wave has traveled.  We'll go over this all a bit more later, but I wanted to introduce it here for you just to get you more familiar with the terminology I'll be using.

Raphel, L. J., Borden, G. J., Harris, K. S. (2007).  Speech science primer:  Physiology, acoustics, perception of speech (5th ed.).  Philadelphia, PA:  Lippincott Williams & Williams.

Physics of Sound Series (Part I): Why do I need to know this stuff?

Because the necessity to resonant over the sound of an orchestra is dependent on vocal tract, and therefore resonance, adjustments.  However, many singers either do not understand resonance, formants, or harmonics well enough, or don't understand how physics relates to physiology well enough, that many misconceptions develop that can greatly hinder vocal progress during training.

Now, I don't mean to generalize, but I do know a lot of singers who roll their eyes at words like "physics" and "math."  In fact, I have had so, so many conversations with musicians about these topics now that I'm taking math and physics courses.  They usually go something like this:  "I can't meet then because my physics class is at that time.  Can you do Monday?"  "Physics?  Why on Earth are you taking Physics?"  "Well, I want to have more detailed knowledge of how the physics of sound and air pressures work so I can understand certain areas of SLP research better."  "Well, good for you.  I know I would never take those classes.  My brain just doesn't work that way."  It is that last sentence that I take the most issue with.  Why, oh why do we as musicians have to demean ourselves when it comes to the potential our brains have to understand something?  Do we even realize the message we're sending out?  I mean, we are the people who learn multiple languages for our roles, we learn some anatomy and physiology of the voice, and we are supposed to have at least some foundational knowledge in harmonics and formants when it comes to resonance.  This is all in addition to music theory, history, performance practice, etc.  Why do we pass off math and physics like it's "over our heads?"  Or maybe we want the world to recognize that we're plenty smart in our own right and should be respected for that (which is true).  Maybe we think that in order for our field to be respected as art we have to separate so thoroughly from science that we must turn our noses up at it.  Maybe we're sick of people in the sciences turning their noses up at us...(I know I'm sick of that).  Maybe we don't want to have to add more stuff to our already extensive list of stuff to know.  Either way, I do wish my fellow musicians would stop looking at me like I've grown a second head when I say I'm enjoying learning calculus and calculus-based physics.  But I digress...

Perhaps most of the issues with math and physics for singers, or just most people in general, comes from the fact that these subjects are very rarely taught well in high school (in the US,) and even in college, for that matter.  Much of the time, teachers in these subjects see the class as some sort of grand IQ test in which student's successes or failures have no bearing on the teacher's ability, or inability, to effectively teach the material.  That's a common fallacy of certain hard-science classes.  (Personally, I liked my calculus's professors take on it:  Success in her class, as far as she was concerned, was totally up to the student's dedication and motivation to keep up with the homework (practice) and get help when needed.)  So we've relegated the teaching of these concepts to a month or so during a vocal pedagogy class.  But maybe, just maybe, voice teachers trying to teach these concepts don't quite give the right amount of time or clarity to these concepts either.  I mean, if you're knowledge doesn't have a strong foundation, it is really easy to get confused when, a few years after your pedagogy class, you've been swamped with new information, new ideas, new research, new teachers, new coaches, etc.  I know I did!

I thought I got plenty of this stuff in my vocal ped. courses.  I thought I had a very good understanding of harmonics, resonance, formants, etc. because I was one of the few in my pedagogy class that was not confused by the lectures or book chapters on it.  I now know I was mistaken.  My mistake came from not having enough of a base-level of understanding in physics to be able to apply these concepts effectively to understanding my own vocal training, and to not get confused a year or two down the road.  There is a huge interaction between the physiology of the voice and how the physics of vocal resonance, as well as the physics of air pressure to breath support, work.  Those connections were simply missing from my pedagogy classes, and, from what I can gather from other conversations with singers, I think it's missing from many singers' academic training as well.

I had such simple misconceptions that I would be embarrassed to admit to in front of anyone with basic physics knowledge, now that I know better.  I see a lot of musicians saying some of these same misconceptions quite frequently, and I really, really want us to stop sounding like complete fools in regards to basic math and basic physics to a large portion of the general population (and not just those in hard sciences, either).  And I know a lot of singers who would really, really like to not sound like fools, but it's just never been explained well enough, or thoroughly enough, to avoid it.  Even if your interest in this might just be cursory, a more thorough understanding of the physics-physiology connection really does help to understand the science behind how the voice, and operatic singing, works and how to apply that knowledge to long-term training.  


So here's how this series is going to work:  I'm not going to get all up in calculus, cause I'm not interested in making this a math course, but I will present some basic algebraic equations.  I will also thoroughly explain these equations so that you can see how the equation is a working representation of how your vocal tract shapes sound.  We'll start with the basics and move up from there, but I'm also going to do my best to detail the interaction between physics and physiology...even if I can't get to that interaction until I get a little further down the series.  If you've ever been confused looking at a spectrogram of your singing, like in PRAAT, then this series should help you out a lot.  It shouldn't be as long as the anatomy and physiology series, so I hope you can hang in here with me.  And ultimately, just like the A&P series, I want this to be a reference tool for singers and teachers to be used whenever you need it.

Sensation vs. Perception: The crux of pedagogical contradictions

Just like Martin Luther King, Jr.,* I have a dream that one day vocal pedagogs will have field-specific, unified terminology that will eliminate the pedagogical confusion so many students experience when moving from one teacher to the next.  However, I'm starting to think this dream is too lofty.  In the subjective field of vocal training, trying to unify the centuries of pedagaogical terminology with the current science of voice might be a little too much of a hurdle to overcome.  I mean, motivated voice students will still desire to read and understand the writings of Lamperti, Garcia, etc. in the context of current voice training, so a complete shift toward unification might alienate the past writings of great pedagogs.

So what are we new pedagogs/voice students supposed to do?  How are we supposed to wade through the old information and understand it in terms of the new?  I think one piece of the puzzle might be to understand the differences between perception and sensation.

I touched a bit on this near the end of my previous post where I talk about what I feel is happening when I am singing, but it is something I've incorporated into my teaching that, I think, many of my students, even the teenagers, seem to appreciate.  One of my high school students had one of her choir teachers give her a few "vocal tips" that seemed to confuse her in terms of what we had been working on in her lesson.  Using this established difference between sensation and perception, I was able to explain rather quickly to this student that we were, in fact, working on those things, we were just calling it something different in our lessons.  This difference has become such an easy way for my students to begin developing a "tranlation" ability, which I find so, so important, since I know for most of them, I will not be their only voice teacher throughout their training.

What is sensation and what is perception?  Sensation is a term used in psychology, as well as anatomy and physiology, to refer to sensory information from the outside world coming into our bodies via the nervous system.  When this information reaches your brain, it processes this information, associates it with memories, etc. through some cognitive processing, and then decides how to act.  This is the process of perception, which happens to be a very individual process.  So sensation (diff. link) is the incoming information, and perception is the interpretation of that incoming information.  This works all the time for all of us in some obvious ways:  If two friends go to see the same movie, both people receive the same incoming information, i.e. the movie, but they might interpret the "take home message" of the movie in two different ways via their individual perceptions.  (How many of us have sent friends articles, etc. where the friend seemed to miss what was, to us, the vital underlying point of the article?  You can now blame their perception for getting it wrong...or yours, if you're humble like that.)

How does this work for pedagogy?  Well, a lot of the differences we encounter in pedagogical terms comes from the vast differences in the perception of proper singing...at least as far as I perceive it.  (Yikes!  This article could quickly become an exercise in circular logic, couldn't it?)  For example:  So much debate has been waged over the "low larynx" issue.  Student 1:  My teacher said my larynx should never move while singing.  Is this right?  Student 2:  Well, my teacher said research has shown that it does move quite a lot and should raise on high notes, so I guess you're teacher is wrong.  Student 1:  But my teacher said historical documents all talk about the importance of a lowered larynx, so are all those singers of the past wrong?  And the debate rages on.  So what's going on here?  How can science point to the opposite of what all the great singers and past teachers say they're doing?  Sensation and perception!  Biologically, the larynx is certainly moving around during singing, and yes, it is raising on high notes.  It's a physics-thing that simply must happen.  However, when laryngeal efficiency has been obtained, the singer feels like their larynx isn't moving at all and the teacher might not see the larynx raising as much in the throat as it used to.  So the singer might perceive that their larynx is stable, but it's just due to how their brain interprets the sensation of laryngeal efficiency throughout their range.

Another example:  #1:  The ribcage must stay elevated and stable!  #2:  The ribcage collapses during exhalation out of necessity since the lungs are getting smaller!  #1:  You're wrong!  Here's a youtube video.  #2:  No, you're wrong!  Here's an article by "Prominent Scientist."  How does sensation and perception help explain this one?  Well, the fact that the chest cavity decreases in size during any exhalation can not be argued.  It's another physics-thing that simply must occur.  But why would so many singers swear up and down that their rib cage is as stable as stable can be and always elevated during singing?  Sensation and perception!  The act of using excess muscular effort to keep the rib cage from lowering too fast sends very different sensation information to the brain than what it's used to.  For most people, the brain interprets this information with the perception that the rib cage is not moving at all, perhaps because the information is so opposite of what the brain is usually getting about the movement of the rib cage.  So you end up with a lot of singers and teachers swearing up and down that the rib cage must not move, when in fact, it must move, but it must move so much more slowly than usual that it feels like it's not moving at all.

I'm sure there are other examples out there, but I cannot think of any at the moment.  If you have had a similar debate about another important pedagogical concept, please let me know.  I'll see if I can answer it using this sensation/perception model of explanation for ya!


*Disclaimer:  This is a dry-humor joke equating my tiny, little dream of unified pedagogical terms to the great deeds accomplished by Dr. King during his lifetime.  I'm pretty much an ant on the mountain of his greatness as far as I'm concerned.  I've just been watching too many 30 Rock reruns to resist the joke. **
**Disclaimer for the disclaimer:  I find dry-humor doesn't always come across online so I felt the need for disclaimer #1.  However, upon reading the over-explanation of the joke in disclaimer #1, I realize the already bad original joke has now been effectively destroyed.  Awesome.