There's a funny thing that happens when you learn a lot of valuable information in a short amount of time. You tend to forget that not everyone is having the same experience you are. I think this is even more pronounced in people who tend to be rather ambitious, like me. I know that in society in general, ambitious people are lauded, but there's a distinction between an ambitious person who has reached a level of success and an ambitious person who is just starting out. The successful person is seen as someone to look up to, and the new student to a discipline is seen as, well, a n00b.
We n00b's, by my definition, tend to be a bit crazy, you see. We geek out to anyone who shows even a tiny bit of interest in what we do. We find ourselves talking far too long about some nuance of our discipline without realizing it. In short, we are awkward and alienating. We're like someone who's just fallen in love, and we just can't help ourselves. However, we usually know we are a little different than others. I think I get it from my father. I once said Dad is a guy who doesn't have "hobbies" he has "obsessions," and, while I do have a few hobbies, I will say that voice science has become an obsession. I can only hope that my cohort of master's students won't mind, and perhaps they will even be the same.
I was like this with opera too, and really, I still am if given the chance. But the years have taught me that very few people can tolerate a singer geeking out about opera for too long before they politely excuse themselves. SLP is a little different, if only because if someone knows what it is, they usually either know someone who went to one, or they went to one themselves. Therefore, they seem to appreciate learning a little more about this profession, usually from the respect they feel toward that SLP who gave their parent a swallow evaluation at the hospital, treated their autistic child, or helped their grandparent after their stroke. For opera singers, though, we're just seen as a novelty, and people don't usually treat you with the same level of respect, perhaps because they've either never been to an opera or have never met an opera singer before. (Or worse yet, perhaps they have and that is why they don't respect them. Parish the thought!) This always ruffles my feathers, because I still strongly feel that, while the value in opera is subjective, it still has value nonetheless. And really, what kind of person are you if you don't at least respect someone for their craft even if you don't see the value in it? (But perhaps the issue lies in the general public not knowing about the craft itself and the training it requires...but I digress.)
What's interesting to me is that while I seem to have gained some respect and/or interest from random people I meet, I've lost a bit with (some) singers, particularly the ones who didn't know me before. Maybe it's that whole "abandoning" the musical profession thing, but I can certainly see that I've become an outsider. You know, someone who no longer understands the demands of the profession, or appreciates what the real professional singers go through. The biggest issue I have with this is I find myself wanting to abandon the singing world altogether. Why go into voice research? Why be interested in treating voice professionals when I get out? They're just going to treat me like I don't understand them anyway. I know this is really just an immature reaction from me generalizing a small portion of the singing population, but I find myself heartbroken all the same. Opera was my first love, profession-wise. I'll never really leave it. I may not train as hard as I used to when I was auditioning, mainly because I no longer have the time, but I still sing. I still remember the training from my master's program and beyond. I know I've gotten a bit rusty, but I can still run the race, even if I can't run it in the Olympics. (Course, I never got a great deal of respect from singers when I was in the profession either, but that's another story...one that I don't really need to write.)
All my new knowledge I've gained in voice science, and it's been significantly more than my pedagogy program, helped me a great deal. I was able to train smarter and more efficiently as a singer and I became a more efficient teacher. I noticed I was able to help my students with a vocal problem within weeks instead of months and months instead of years. I was a good teacher before, but I'm a better teacher now. But, I've gain new, more specific terminology that makes it harder to communicate with other voice teachers. I can see a rift forming in my mind just as it is forming in those singers who see me as an outsider.
That rift is the burden of knowledge. I know that sounds pompous, but it really isn't. On the contrary, it is a lonely place. It is the divide that comes when you forget exactly how much your target audience knows and how much they don't know. If you assume they know more than they do, you talk over their heads and seem like a pompous blow-hard who just wants to show them up intellectually. Assume they know less, and you seem condescending. As I integrate new knowledge, it solidifies, and I forget what it is I didn't know two years ago. Everything I've gained is just elementary stuff to the professors and licenced SLPs in my new field, and as such, I approach a lot of this as if it is elementary. However, some of this stuff is way beyond what some singers learn in pedagogy courses, so forgetting that makes the rift larger. And yet for others it is not all that far off; it really just depends on the school. So how does one begin to talk about it without falling into that rift? Maybe I'll never learn to find the balance. To talk in a way that doesn't alienate or deride and to be seen as a colleague to singers instead of a traitor and offender. And maybe I'll never stop being an outsider. I hope I find that balance someday, though, cause I would rather be of help to others (who wish for it) than to drift away in the rift.
Saturday, June 16, 2012
Friday, June 15, 2012
One journey ends, another begins
Well, what the heck have I been up to! It's been a really long time since I posted last, huh? Where did I disappear to? Answer: School. Last semester literally sucked up all the time I had. Long story short: I was taking all non-SLP related courses that left me a bit burnt out. Sorry I disappeared like that, though!
Sometimes, I hear from singers thinking about getting into SLP themselves. I usually tell them to prepare for a time-intensive, difficult journey, but I realized that the difficulty is one area of my journey I had kind of been avoiding on here. So, truth time. This post is all about that point from deciding to be an SLP to the point of beginning graduate school in it, which for me, will be this August.
My journey to being a speech pathologist hasn't been a smooth one. I'm actually just going to be starting my master's program this coming year. Which, if you've been counting, means I've been taking undergraduate courses for two years now just to get to the point where I could do the two-year master's program. I honestly did not expect it to take this long.
Rewind to fall of 2010. I decided to become an SLP. I applied to my local university, since they have a three-year program for non-SLP undergraduate majors. I didn't get in, and that kinda sucked. I mean, I had finally gotten that fire-in-the-belly feeling about my life direction, so not getting in felt like just another failure on top of all the music-world failures I had accumulated over the years. Ain't that how it goes, though? You feel like life is getting back "on track" after a set-back and, low and behold, there's another set-back waiting right around the corner. I didn't want to wait any longer! I wanted momentum in my life! I wanted direction...but I got rejection. Good times.
See, I knew I had at least one year of undergraduate courses I would need to complete before I could start a clinical program. That's just how it goes for folks who weren't SLP undergraduates, but the day after the rejection letter came, the school told me their "leveling" program (as it's called) was full already. Luckily, they also informed me there was another leveling program at a state school in *big city* nearby. I applied to the state school's program right away, and I was registered for fall classes by the end of the week. Whew! Momentum was back, and I was on my way! *happy dance*
During that fall semester, I applied to about six graduate schools across the nation. My then-fiance and I tried to line up our schools, since he was going to graduate school in a STEM field. We played the waiting game, and it turned out that I got into one program out of the six. (Turns out, SLP is kinda hot right now just cause there are still jobs in that field, so schools are getting waaaaayy more applicants than it used to, but slots are still quite limited. Therefore, getting into grad school has become quite the challenge to many of us levelers out there.) However, our problem was that the program wasn't in a city where he got admitted. In addition to that, the cost of that particular program was ridiculous! About two-thirds more than most SLP programs, and the city where it was located is one of the most expensive to live in. Meanwhile, my SO got admitted with full funding and a stipend to a top-ten program in his field, which also happened to be in a town with a low cost of living. So, I turned down the one crazy-expensive program and we headed out to where he was going to school.
I took a gamble on new plan: Take some science and math courses, which I would need eventually for my licence anyway, and apply to the two programs in our new state. I reviewed math, with the help of my now-husband, and passed my way into Calculus I, and I also took a psychology course that fall I would need later. This past spring semester, I took Calculus II, Introduction to Mechanics (which what calculus-based Physics I is called here), and another psychology course online. Do SLPs need calculus and calc-based physics? No. But I took them because during my leveling program, I starting thinking I would actually continue to get my PhD after my master's degree, and strong math/physics knowledge would help in one of my research interests immensely. (I'm kinda an over-achiever like that. And besides, I also figured taking some classes beyond what most SLP undergrads take would set me apart, so I figured it was a win-win...as long as I got good grades.)
And luckily, my gamble paid off! I got into both schools! Yay! *Big happy dance* So now, here I sit. Waiting to actually begin my journey of becoming an SLP. Well, I suppose that's not entirely true, since I've spent two years studying to get here, but I sorta feels true. It's been a much longer journey just to begin the privilege of clinical training than I ever thought it would be. If this journey was shown in some movie-montage, it would be probably be a very boring montage; mostly consisting of me sitting and studying at a coffee shop, at home, and at school. (Huh...I guess there's a good reason Hollywood has stayed away from the study-themed montage.) If I had known it would take this long would I have done it? I'm honestly not sure, but now that I've learned what I've learned so far, I'm glad I did it. If I have one talent and passion for any one thing it's learning. (I. am. a. geek.)
I'm sitting here with aspirations of greatness...not too unlike my 18-year-old singer-self back in undergraduate days. The only difference is, my 18-year-old self was doing her best not to be crippled by the fear of failure, but my thirty-something self has no such fear. Not because failure couldn't happen, I know enough of probability to never say never, but because experience as taught me that failure really isn't something to fear. I know, I know, could I be more cliche? Here's the distinction I really want to draw for you, though: Not fearing failure isn't the same as inviting failure. I'd be quite content if failure never showed up ever again and I'm going to plan my ass off and work my ass off to keep it at bay. But by not fearing it, I can look at any challenge square in the face and say, "Bring it. Cause I'm all in." Cliche? Yes. Freeing? Absolutely!
Sometimes, I hear from singers thinking about getting into SLP themselves. I usually tell them to prepare for a time-intensive, difficult journey, but I realized that the difficulty is one area of my journey I had kind of been avoiding on here. So, truth time. This post is all about that point from deciding to be an SLP to the point of beginning graduate school in it, which for me, will be this August.
My journey to being a speech pathologist hasn't been a smooth one. I'm actually just going to be starting my master's program this coming year. Which, if you've been counting, means I've been taking undergraduate courses for two years now just to get to the point where I could do the two-year master's program. I honestly did not expect it to take this long.
Rewind to fall of 2010. I decided to become an SLP. I applied to my local university, since they have a three-year program for non-SLP undergraduate majors. I didn't get in, and that kinda sucked. I mean, I had finally gotten that fire-in-the-belly feeling about my life direction, so not getting in felt like just another failure on top of all the music-world failures I had accumulated over the years. Ain't that how it goes, though? You feel like life is getting back "on track" after a set-back and, low and behold, there's another set-back waiting right around the corner. I didn't want to wait any longer! I wanted momentum in my life! I wanted direction...but I got rejection. Good times.
See, I knew I had at least one year of undergraduate courses I would need to complete before I could start a clinical program. That's just how it goes for folks who weren't SLP undergraduates, but the day after the rejection letter came, the school told me their "leveling" program (as it's called) was full already. Luckily, they also informed me there was another leveling program at a state school in *big city* nearby. I applied to the state school's program right away, and I was registered for fall classes by the end of the week. Whew! Momentum was back, and I was on my way! *happy dance*
During that fall semester, I applied to about six graduate schools across the nation. My then-fiance and I tried to line up our schools, since he was going to graduate school in a STEM field. We played the waiting game, and it turned out that I got into one program out of the six. (Turns out, SLP is kinda hot right now just cause there are still jobs in that field, so schools are getting waaaaayy more applicants than it used to, but slots are still quite limited. Therefore, getting into grad school has become quite the challenge to many of us levelers out there.) However, our problem was that the program wasn't in a city where he got admitted. In addition to that, the cost of that particular program was ridiculous! About two-thirds more than most SLP programs, and the city where it was located is one of the most expensive to live in. Meanwhile, my SO got admitted with full funding and a stipend to a top-ten program in his field, which also happened to be in a town with a low cost of living. So, I turned down the one crazy-expensive program and we headed out to where he was going to school.
I took a gamble on new plan: Take some science and math courses, which I would need eventually for my licence anyway, and apply to the two programs in our new state. I reviewed math, with the help of my now-husband, and passed my way into Calculus I, and I also took a psychology course that fall I would need later. This past spring semester, I took Calculus II, Introduction to Mechanics (which what calculus-based Physics I is called here), and another psychology course online. Do SLPs need calculus and calc-based physics? No. But I took them because during my leveling program, I starting thinking I would actually continue to get my PhD after my master's degree, and strong math/physics knowledge would help in one of my research interests immensely. (I'm kinda an over-achiever like that. And besides, I also figured taking some classes beyond what most SLP undergrads take would set me apart, so I figured it was a win-win...as long as I got good grades.)
And luckily, my gamble paid off! I got into both schools! Yay! *Big happy dance* So now, here I sit. Waiting to actually begin my journey of becoming an SLP. Well, I suppose that's not entirely true, since I've spent two years studying to get here, but I sorta feels true. It's been a much longer journey just to begin the privilege of clinical training than I ever thought it would be. If this journey was shown in some movie-montage, it would be probably be a very boring montage; mostly consisting of me sitting and studying at a coffee shop, at home, and at school. (Huh...I guess there's a good reason Hollywood has stayed away from the study-themed montage.) If I had known it would take this long would I have done it? I'm honestly not sure, but now that I've learned what I've learned so far, I'm glad I did it. If I have one talent and passion for any one thing it's learning. (I. am. a. geek.)
I'm sitting here with aspirations of greatness...not too unlike my 18-year-old singer-self back in undergraduate days. The only difference is, my 18-year-old self was doing her best not to be crippled by the fear of failure, but my thirty-something self has no such fear. Not because failure couldn't happen, I know enough of probability to never say never, but because experience as taught me that failure really isn't something to fear. I know, I know, could I be more cliche? Here's the distinction I really want to draw for you, though: Not fearing failure isn't the same as inviting failure. I'd be quite content if failure never showed up ever again and I'm going to plan my ass off and work my ass off to keep it at bay. But by not fearing it, I can look at any challenge square in the face and say, "Bring it. Cause I'm all in." Cliche? Yes. Freeing? Absolutely!
Sunday, February 19, 2012
The Physics of Sound: Resonance and Standing Waves
So what does happen when two sound waves are in phase with one another? The two waves constructively interfere with one another to result in one wave that this double the amplitude of the two waves. Basically, they both add up like some awesome crime-fighting team...and they...help people hear and stuff. (Yeah...I don't know where I was going with that metaphor.) Anyway, to better understand this, let's talk a little more about the phenomenon of interference.
Interference is when two waves sorta "line up" together. Depending on how they "line up," the two waves combine to form one wave that is either of lesser or greater amplitude than the two waves were just on their own. Think of it like this: If one wave is going along with an amplitude of, let's say, 2 dB, and it meets up with another wave that's out of phase with this first wave, and the second wave's amplitude is 1.5 dB, then the resultant effect will be the 1.5 dB wave "canceling out" some of the amplitude of the first wave. So you'd get a net result of a 0.5 dB sound wave. If, however, the 2 dB sound wave meets up with a wave that's totally in phase with it, and this wave is going along at 2 dB, the resultant wave will be 4 dB. So, yes, interference is very much like when you hang out with that soul-sucking person you really shouldn't be around (destructive) or that person who just makes you feel great (constructive). (That's a super-basic way to represent interference mathematically, and the real math is much, much more detailed and complex, but it's just there to give you an idea. So please don't go around thinking it's just addition and subtraction when scientists are figuring out interference. It'd be a bit like those people who think a graduate degree in vocal performance just means you sing karaoke all day and get a degree for it.)
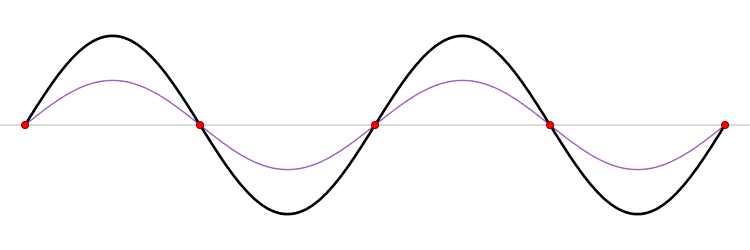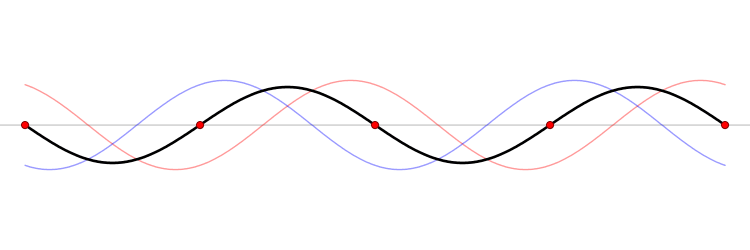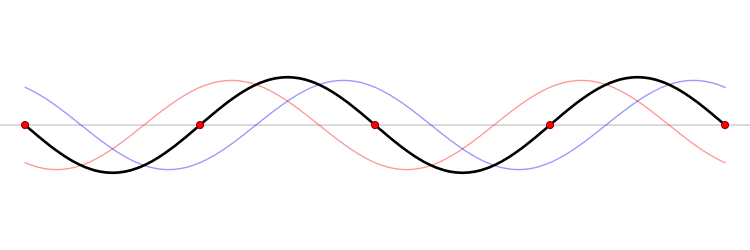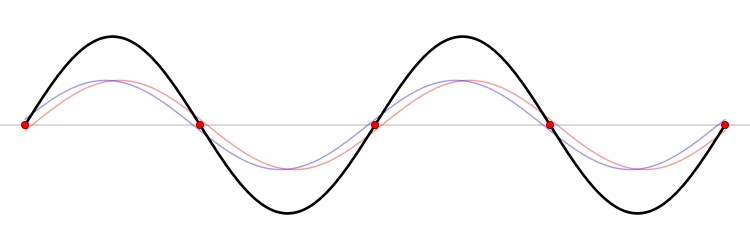
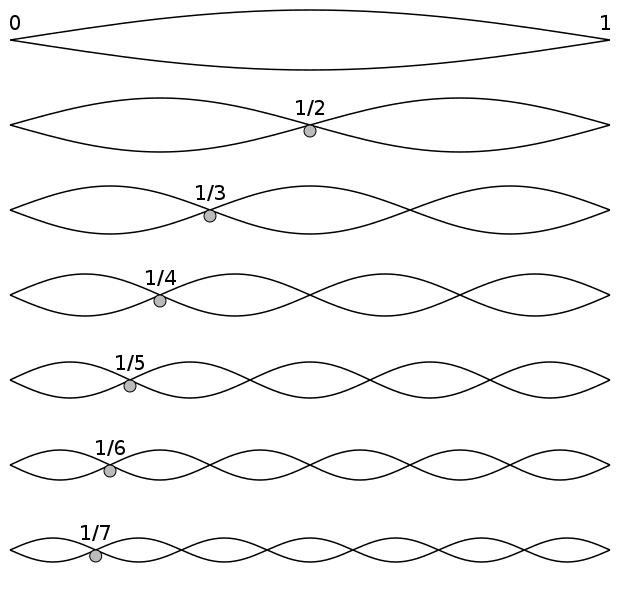
Sound waves travel along just fine until they hit a boundary. When that happens, the waves bounce off the boundary and become reflected waves. The initial wave, called the incident wave, can meet up with the reflected wave where the two waves interfere with one another to form a new wave that is the sum of the other two waves. This is called the principle of superposition. (I know I'm getting a bit redundant, but hang with me here.) If, during superposition, two waves meet up that are completely in phase, the result is a standing wave.
As you can see above, one type of standing wave doesn't travel anywhere. It stays in the same place constantly. This results in areas where the displacement is zero, called nodes (shown by the red dots above), and areas of maximum displacement called antinodes (the tall peaks and valleys above). So the constructive interference of an initial wave meeting up with a reflective wave to form a standing wave looks something like this:
But how do standing waves that don't go anywhere contribute to a singer's resonance? Well, that question is kinda jumping a bit farther ahead than where we are now. For now, just think about standing waves on a medium that is fixed on both ends, like a string. Ever played with a string or necklace where you bounce the string up and down? If you have, you actually formed a standing wave at the string's first resonant frequency, called the fundamental frequency. But the string does have other frequencies it could resonant at, called overtones.
But why am I talking about strings? What do strings have to do with vocal resonance? Think about it a second: What acts like vibrating strings with fixed ends when we speak or sing? Yup, the vocal folds. But, the vocal folds vibrate in patterns that are much more complex than just a single string. Remember how the air opens them from the bottom to the top, due to subglottal air pressure, and then the folds get sucked in laterally because of the Bernoulli effect? The resulting wave pattern is very intricate,which results in a complex waveform (multiple simple sine waves going out at once) being produced at the level of the vocal folds. The fundamental frequency and all of the overtones of the human voice originate at the level of the vocal folds.
*That last bit is very, very important, and it seems to be where a lot of singers get very confused...usually not due to any fault of their own. The vocal tract absolutely cannot create sound waves or overtones to those sound waves: Not the singer's formant, not the harmonics, not any of it. All of the frequencies picked up by a spectrograph originate from vocal fold vibration. The vocal tract only acts as a filter for the frequencies sent out by the vibrational pattern of the vocal folds. And that's where we'll pick up next time!
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
Interference is when two waves sorta "line up" together. Depending on how they "line up," the two waves combine to form one wave that is either of lesser or greater amplitude than the two waves were just on their own. Think of it like this: If one wave is going along with an amplitude of, let's say, 2 dB, and it meets up with another wave that's out of phase with this first wave, and the second wave's amplitude is 1.5 dB, then the resultant effect will be the 1.5 dB wave "canceling out" some of the amplitude of the first wave. So you'd get a net result of a 0.5 dB sound wave. If, however, the 2 dB sound wave meets up with a wave that's totally in phase with it, and this wave is going along at 2 dB, the resultant wave will be 4 dB. So, yes, interference is very much like when you hang out with that soul-sucking person you really shouldn't be around (destructive) or that person who just makes you feel great (constructive). (That's a super-basic way to represent interference mathematically, and the real math is much, much more detailed and complex, but it's just there to give you an idea. So please don't go around thinking it's just addition and subtraction when scientists are figuring out interference. It'd be a bit like those people who think a graduate degree in vocal performance just means you sing karaoke all day and get a degree for it.)
Sound waves travel along just fine until they hit a boundary. When that happens, the waves bounce off the boundary and become reflected waves. The initial wave, called the incident wave, can meet up with the reflected wave where the two waves interfere with one another to form a new wave that is the sum of the other two waves. This is called the principle of superposition. (I know I'm getting a bit redundant, but hang with me here.) If, during superposition, two waves meet up that are completely in phase, the result is a standing wave.
 |
 |
| The red and blue waves meet up to form the standing wave in black. Other cool animations can be found here and here. |
 |
| First fundamental and first six overtones of a string |
*That last bit is very, very important, and it seems to be where a lot of singers get very confused...usually not due to any fault of their own. The vocal tract absolutely cannot create sound waves or overtones to those sound waves: Not the singer's formant, not the harmonics, not any of it. All of the frequencies picked up by a spectrograph originate from vocal fold vibration. The vocal tract only acts as a filter for the frequencies sent out by the vibrational pattern of the vocal folds. And that's where we'll pick up next time!
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
Sunday, February 12, 2012
Physics of Sound Series: The Waveform (or, What the Heck am I Looking At?)
We now know that a sound wave is made up of moments of compression and rarefaction, and we know a little bit about a waveform as well. But there are other parts to a wave that we need to know about before we get into just what resonance really is. Those parts are: Period, frequency, amplitude, phase, and wavelength.
No doubt, you've heard of some of these before. Frequency and amplitude, in particular, get a lot of attention in the music world. A lot of times, we talk about frequency and amplitude as synonymous with pitch and loudness, and for most purposes they are. However, when I talk about frequency and amplitude, I'm going to be referring to the actual physical properties of the sound wave (or waves), meaning the parts of the wave that can be measured with proper instrumentation and then studied. Therefore, frequency and amplitude are objective measurements. Pitch and loudness are usually associated with the perceptual properties of the wave, i.e. just how loud or how high/low a person perceives that sound differs from person to person (and from ear to ear, for that matter); so pitch and loudness cannot be measured per se, but rather discussed subjectively. (And remember from my previous post: Anytime I'm talking about perception, I'm talking about the interaction from a sensory signal with a person's higher cognitive functions and life experiences. Therefore, perception is always subjective.)
When you look at the waveform of a basic sine wave (the red line) shown above, you'll see that it has a repeating pattern. The number of repeats of this pattern in a given amount of time is called the frequency of the wave. This is usually given in Hertz, but can also be stated as the number of cycles per second of the wave pattern. (See, it was originally called cycles per second (cps), but then the International Electrotechnical Commission (IEC) decided to honor Heinrich Hertz's contribution to the field of electromagnetism, so they gave him a unit of measurement, cps, and called it Hertz (Hz). Scientists are always re-naming units to honor the great contributors to the field. Sorta like how medical terminology is also littered with the names of big anatomy contributors, etc.) So, for the famous A440 that orchestra's (supposedly) tune to, the frequency is 440 cycles per second, or 440 Hz. In math terms, frequency is shown by: frequency = velocity over wavelength (f = v/λ). Sounds pretty fancy, but the reason I'm putting this here is because the period of a wave is related to the frequency. The period is how long it takes for one cycle of the wave pattern to complete itself. So if the frequency could be shown as: 1/period, then the period is shown by: 1/frequency. Seems like we're talking about the same thing, but in general, the frequency refers to how often the wave pattern is repeating itself where the period refers to how long it takes for one pattern of the wave to complete itself. Why do we bother with this distinction? Well, because it comes in really handy for mathematical analysis of wave patterns. Why should singers bother to know about this? Because...well...I'll get there for ya. (Besides, if your ever playing around with PRAAT or some other spectrograph software, you'll probably see options for period or frequency change, and you might want to know what you're changing out as you play around.)
Wavelength corresponds to the distance one cycle of the wave travels. Slower frequencies have longer wavelengths, so one cycle of A440 travels double the distance through the atmosphere than A880. (In the above equations, wavelength is represented by that funny-looking symbol, which turns out to be the Greek letter lambda. So now, when you poke around wikipedia and see frequency equations, you'll know some of what you're looking at.)
The amplitude of a wave corresponds to it's perceptual loudness, and is related to the amount of displacement the air particles go through in the sound wave. Because it has to do with how far each particle is being "pushed," amplitude represents the atmospheric pressure of a sound wave, and is measured in decibels (dB). In the waveform shown above, amplitude is represented on the vertical axis. So if the sine wave had a higher amplitude, it would have taller peeks and lower valleys, going past the 1.00 marked above. Even though amplitude of sound is represented by this vertical displacement on the waveform, in longitudinal waves, the displacement in the real world is happening horizontally. This is different for other wave types, like light, but the math and the graphical representations are the same. (I just want to point that out because it's easy to misinterpret the sound waves from your mouth as looking just like the waveform representation, but if we could see the sound wave, it would like more like the animation here. That's kinda important to remember once we get to the anatomy of the ear and the role the ear drum plays in hearing. And, oh yeah! I'm going to get into the anatomy of the ear and how it plays a role in resonance as well, for both the audience and the singer!)
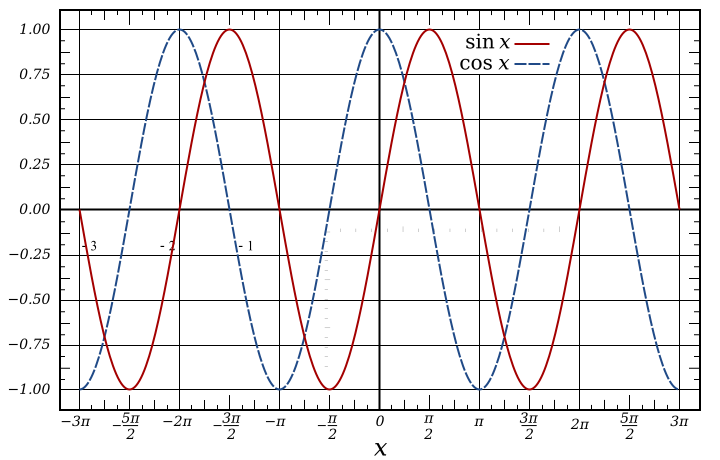
Phase is where we start to get into some important stuff when it comes to understanding resonance, and especially the phenomenon of standing waves. The phase of the sine wave in the above picture basically is where in the cycle the wave starts when you're looking at the vertical axis. Let's look at it more closely:
See how the sine wave is passing through the vertical axis where the horizontal line equals 0? Now look at the cosine wave (blue, dotted line). Cosine is passing through that vertical axis where a horizontal line equals 1. So the phase of the sine wave is not the same as the phase of the cosine wave. The fancy way of saying that is that cosine has a different phase shift than sine. In fact, that's actually the main difference between sine and cosine: The phase shift between the two.
Phase is really, really important because if you have two sound waves that are out-of-shift like this:
You'll see how when one wave has a peek in its amplitude, the other wave has a valley, or a negative amplitude. This means that when one wave is in it's period of compression, the other is in rarefaction. The result is that these two waves actually cancel each other out, because if the atmospheric pressure is equally positive in one wave while the pressure is equally negative from the other wave, the two pressure differences cancel each other out. 1-1=0, right? Crazy, huh?
But what happens when two sound waves are perfectly in phase? What if you've got 1 + 1 instead of 1 -1? That's where the phenomenon of standing waves comes in, and that's what we'll start up with next time. Stay tuned!
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
No doubt, you've heard of some of these before. Frequency and amplitude, in particular, get a lot of attention in the music world. A lot of times, we talk about frequency and amplitude as synonymous with pitch and loudness, and for most purposes they are. However, when I talk about frequency and amplitude, I'm going to be referring to the actual physical properties of the sound wave (or waves), meaning the parts of the wave that can be measured with proper instrumentation and then studied. Therefore, frequency and amplitude are objective measurements. Pitch and loudness are usually associated with the perceptual properties of the wave, i.e. just how loud or how high/low a person perceives that sound differs from person to person (and from ear to ear, for that matter); so pitch and loudness cannot be measured per se, but rather discussed subjectively. (And remember from my previous post: Anytime I'm talking about perception, I'm talking about the interaction from a sensory signal with a person's higher cognitive functions and life experiences. Therefore, perception is always subjective.)
 |
| Yup, those are the same sine and cosine functions from trigonometry that you see on your calculator. |
Wavelength corresponds to the distance one cycle of the wave travels. Slower frequencies have longer wavelengths, so one cycle of A440 travels double the distance through the atmosphere than A880. (In the above equations, wavelength is represented by that funny-looking symbol, which turns out to be the Greek letter lambda. So now, when you poke around wikipedia and see frequency equations, you'll know some of what you're looking at.)
The amplitude of a wave corresponds to it's perceptual loudness, and is related to the amount of displacement the air particles go through in the sound wave. Because it has to do with how far each particle is being "pushed," amplitude represents the atmospheric pressure of a sound wave, and is measured in decibels (dB). In the waveform shown above, amplitude is represented on the vertical axis. So if the sine wave had a higher amplitude, it would have taller peeks and lower valleys, going past the 1.00 marked above. Even though amplitude of sound is represented by this vertical displacement on the waveform, in longitudinal waves, the displacement in the real world is happening horizontally. This is different for other wave types, like light, but the math and the graphical representations are the same. (I just want to point that out because it's easy to misinterpret the sound waves from your mouth as looking just like the waveform representation, but if we could see the sound wave, it would like more like the animation here. That's kinda important to remember once we get to the anatomy of the ear and the role the ear drum plays in hearing. And, oh yeah! I'm going to get into the anatomy of the ear and how it plays a role in resonance as well, for both the audience and the singer!)
Phase is where we start to get into some important stuff when it comes to understanding resonance, and especially the phenomenon of standing waves. The phase of the sine wave in the above picture basically is where in the cycle the wave starts when you're looking at the vertical axis. Let's look at it more closely:
See how the sine wave is passing through the vertical axis where the horizontal line equals 0? Now look at the cosine wave (blue, dotted line). Cosine is passing through that vertical axis where a horizontal line equals 1. So the phase of the sine wave is not the same as the phase of the cosine wave. The fancy way of saying that is that cosine has a different phase shift than sine. In fact, that's actually the main difference between sine and cosine: The phase shift between the two.
Phase is really, really important because if you have two sound waves that are out-of-shift like this:
 |
| Look at the three middle waves to see the phase difference. |
But what happens when two sound waves are perfectly in phase? What if you've got 1 + 1 instead of 1 -1? That's where the phenomenon of standing waves comes in, and that's what we'll start up with next time. Stay tuned!
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
Friday, February 10, 2012
Physics of Sound Series: The Acoustic Wave
I always have the hardest time starting up these series, because I spend a lot of time trying to figure out where to start. I always know what the ending conclusion should be, but what's the beginning? What's basic without being too basic? So I'm going to start out where I think it should start out, but if I'm not being basic enough, please feel free to post any questions you may have.
Everybody always talks about resonance in the singing world. Resonance, resonance, resonance. Let's face it, as opera singers, we're pretty obsessed about it. And why wouldn't we be? It is, after all, the key to how opera singing works. It is exactly how we are able to sing over an orchestra for hours at a time without hurting our voices. The only issue I have with all this resonance talk is that it is painfully obvious that (some) singers have absolutely no clue what resonance really is. It often gets talked about as a subjective thing that changes from person to person. This is understandable given that so much of the sensation of singing is subjective, and therefore, how we teach singing is subjective. It only makes sense that singers would start to think everything about singing is subjective somehow. However, when we take something from the hard sciences, like resonance, and think of it as something that acts differently from person to person, as if it doesn't follow the laws of nature, we kinda sound like fools. The other issue with all this resonance-as-subjective talk is that it makes what could be very clear pedagogy very fuzzy and confusing. So, in order to fully understand what resonance is and how it can help us sing better, let's start with how a single sound wave works.
There are a lot of things in nature that function like waves: Light, sound, the water in your bathtub...(okay, fine, ocean water too), but what exactly does that mean for sound to have a wave-like pattern of behavior? Well, here's the definition of a wave from physics: "a disturbance (an oscillation) that travels through space and time, accompanied by a transfer of energy...often with no permanent displacement of the particles of the medium (Wikipedia)." Sounds pretty fancy, am I right? But it does make a lot of sense. If you drop a rock straight down into a body of still water, the rock disturbs the water's stillness causing a rippling of waves that travel out to the edges of that body of water. Energy was transferred from the rock to the water which then traveled out to the edges of the body of water. The water itself, though, will return to being still, i.e. it doesn't just keep traveling away from the rock until there's no water left, so there wasn't a permanent displacement of the particles of that water (you know, H2O).
So what's the "medium" for sound waves? Air particles! All the lovely little air particles that make up our atmosphere is the medium for all the sound waves we hear, and the ones we don't hear too (i.e. ultrasound, infrasound, etc). For our purposes, we'll think of a sound wave as beginning with air particles at rest. An external force then comes along and sets those particles in motion (like when the electric slide is played at a wedding...sorry, couldn't resist.) Anyways, let's imagine those particles are all lined up nicely next to one another. The particles in row A, the ones closest to the external force, then get "pushed" up towards the particles in row B. This is where we say the row A particles are "compressed" against row B, which then gets pushed up against row C, and so on. (Anyone who's ever seen elementary-school kids line up for recess knows what I'm talking about here.) So while each row is going into it's period of compression with the particles in front of it, the rows that have already been compressed then go into a period of rarefaction. This would be when row A, after compressing with row B, swings back towards it's resting position. But instead of landing at rest, row A actually over-shoots its resting position and ends up being spaced out farther from the row B particles. If we want to get even more specific here, the property of inertia for those particles causes row A to compress with row B, then the property of elasticity over-takes row A's inertia, sending the particles back towards resting. However, the property of inertia for that row of particles then over-takes elasticity and causes row A to over-shoot it's resting position. But, don't fear, cause elasticity will over-take inertia and send row A back to towards resting. This process will repeat itself until row A is again completely at rest. Sounds complicated, but if you've ever set a pendulum into motion and watched until it came to rest again, you've seen this same action at work. (*Edit to add: This pattern of motion is called simple harmonic motion and is actually what pretty much everything in nature can be reduced to.)
This pattern of compression and rarefaction makes up what we call the sound wave. This is why sound waves are sometimes called compression waves, but more commonly, they are called longitudinal waves. (If you clicked on the link I had above on "compressed," you probably saw that coming.) I encourage you to go ahead over to the link for longitudinal waves, because there are some very nice animations over there for you to see these waves in action.
One last thing before I sign off: This pattern of compression and rarefaction is often graphically represented as a waveform. Typically, waveforms are set on a typical Cartesian coordinate system (the graphs with x and y from math class), with the y, or vertical, axis representing the amount of displacement, which also happens to be the amplitude of the sound wave, and the horizontal axis representing the amount of time the wave has traveled. We'll go over this all a bit more later, but I wanted to introduce it here for you just to get you more familiar with the terminology I'll be using.
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
Everybody always talks about resonance in the singing world. Resonance, resonance, resonance. Let's face it, as opera singers, we're pretty obsessed about it. And why wouldn't we be? It is, after all, the key to how opera singing works. It is exactly how we are able to sing over an orchestra for hours at a time without hurting our voices. The only issue I have with all this resonance talk is that it is painfully obvious that (some) singers have absolutely no clue what resonance really is. It often gets talked about as a subjective thing that changes from person to person. This is understandable given that so much of the sensation of singing is subjective, and therefore, how we teach singing is subjective. It only makes sense that singers would start to think everything about singing is subjective somehow. However, when we take something from the hard sciences, like resonance, and think of it as something that acts differently from person to person, as if it doesn't follow the laws of nature, we kinda sound like fools. The other issue with all this resonance-as-subjective talk is that it makes what could be very clear pedagogy very fuzzy and confusing. So, in order to fully understand what resonance is and how it can help us sing better, let's start with how a single sound wave works.
There are a lot of things in nature that function like waves: Light, sound, the water in your bathtub...(okay, fine, ocean water too), but what exactly does that mean for sound to have a wave-like pattern of behavior? Well, here's the definition of a wave from physics: "a disturbance (an oscillation) that travels through space and time, accompanied by a transfer of energy...often with no permanent displacement of the particles of the medium (Wikipedia)." Sounds pretty fancy, am I right? But it does make a lot of sense. If you drop a rock straight down into a body of still water, the rock disturbs the water's stillness causing a rippling of waves that travel out to the edges of that body of water. Energy was transferred from the rock to the water which then traveled out to the edges of the body of water. The water itself, though, will return to being still, i.e. it doesn't just keep traveling away from the rock until there's no water left, so there wasn't a permanent displacement of the particles of that water (you know, H2O).
So what's the "medium" for sound waves? Air particles! All the lovely little air particles that make up our atmosphere is the medium for all the sound waves we hear, and the ones we don't hear too (i.e. ultrasound, infrasound, etc). For our purposes, we'll think of a sound wave as beginning with air particles at rest. An external force then comes along and sets those particles in motion (like when the electric slide is played at a wedding...sorry, couldn't resist.) Anyways, let's imagine those particles are all lined up nicely next to one another. The particles in row A, the ones closest to the external force, then get "pushed" up towards the particles in row B. This is where we say the row A particles are "compressed" against row B, which then gets pushed up against row C, and so on. (Anyone who's ever seen elementary-school kids line up for recess knows what I'm talking about here.) So while each row is going into it's period of compression with the particles in front of it, the rows that have already been compressed then go into a period of rarefaction. This would be when row A, after compressing with row B, swings back towards it's resting position. But instead of landing at rest, row A actually over-shoots its resting position and ends up being spaced out farther from the row B particles. If we want to get even more specific here, the property of inertia for those particles causes row A to compress with row B, then the property of elasticity over-takes row A's inertia, sending the particles back towards resting. However, the property of inertia for that row of particles then over-takes elasticity and causes row A to over-shoot it's resting position. But, don't fear, cause elasticity will over-take inertia and send row A back to towards resting. This process will repeat itself until row A is again completely at rest. Sounds complicated, but if you've ever set a pendulum into motion and watched until it came to rest again, you've seen this same action at work. (*Edit to add: This pattern of motion is called simple harmonic motion and is actually what pretty much everything in nature can be reduced to.)
This pattern of compression and rarefaction makes up what we call the sound wave. This is why sound waves are sometimes called compression waves, but more commonly, they are called longitudinal waves. (If you clicked on the link I had above on "compressed," you probably saw that coming.) I encourage you to go ahead over to the link for longitudinal waves, because there are some very nice animations over there for you to see these waves in action.
One last thing before I sign off: This pattern of compression and rarefaction is often graphically represented as a waveform. Typically, waveforms are set on a typical Cartesian coordinate system (the graphs with x and y from math class), with the y, or vertical, axis representing the amount of displacement, which also happens to be the amplitude of the sound wave, and the horizontal axis representing the amount of time the wave has traveled. We'll go over this all a bit more later, but I wanted to introduce it here for you just to get you more familiar with the terminology I'll be using.
Raphel, L. J., Borden, G. J., Harris, K. S. (2007). Speech science primer: Physiology, acoustics, perception of speech (5th ed.). Philadelphia, PA: Lippincott Williams & Williams.
Wednesday, January 11, 2012
Physics of Sound Series (Part I): Why do I need to know this stuff?
Because the necessity to resonant over the sound of an orchestra is dependent on vocal tract, and therefore resonance, adjustments. However, many singers either do not understand resonance, formants, or harmonics well enough, or don't understand how physics relates to physiology well enough, that many misconceptions develop that can greatly hinder vocal progress during training.
Now, I don't mean to generalize, but I do know a lot of singers who roll their eyes at words like "physics" and "math." In fact, I have had so, so many conversations with musicians about these topics now that I'm taking math and physics courses. They usually go something like this: "I can't meet then because my physics class is at that time. Can you do Monday?" "Physics? Why on Earth are you taking Physics?" "Well, I want to have more detailed knowledge of how the physics of sound and air pressures work so I can understand certain areas of SLP research better." "Well, good for you. I know I would never take those classes. My brain just doesn't work that way." It is that last sentence that I take the most issue with. Why, oh why do we as musicians have to demean ourselves when it comes to the potential our brains have to understand something? Do we even realize the message we're sending out? I mean, we are the people who learn multiple languages for our roles, we learn some anatomy and physiology of the voice, and we are supposed to have at least some foundational knowledge in harmonics and formants when it comes to resonance. This is all in addition to music theory, history, performance practice, etc. Why do we pass off math and physics like it's "over our heads?" Or maybe we want the world to recognize that we're plenty smart in our own right and should be respected for that (which is true). Maybe we think that in order for our field to be respected as art we have to separate so thoroughly from science that we must turn our noses up at it. Maybe we're sick of people in the sciences turning their noses up at us...(I know I'm sick of that). Maybe we don't want to have to add more stuff to our already extensive list of stuff to know. Either way, I do wish my fellow musicians would stop looking at me like I've grown a second head when I say I'm enjoying learning calculus and calculus-based physics. But I digress...
Perhaps most of the issues with math and physics for singers, or just most people in general, comes from the fact that these subjects are very rarely taught well in high school (in the US,) and even in college, for that matter. Much of the time, teachers in these subjects see the class as some sort of grand IQ test in which student's successes or failures have no bearing on the teacher's ability, or inability, to effectively teach the material. That's a common fallacy of certain hard-science classes. (Personally, I liked my calculus's professors take on it: Success in her class, as far as she was concerned, was totally up to the student's dedication and motivation to keep up with the homework (practice) and get help when needed.) So we've relegated the teaching of these concepts to a month or so during a vocal pedagogy class. But maybe, just maybe, voice teachers trying to teach these concepts don't quite give the right amount of time or clarity to these concepts either. I mean, if you're knowledge doesn't have a strong foundation, it is really easy to get confused when, a few years after your pedagogy class, you've been swamped with new information, new ideas, new research, new teachers, new coaches, etc. I know I did!
I thought I got plenty of this stuff in my vocal ped. courses. I thought I had a very good understanding of harmonics, resonance, formants, etc. because I was one of the few in my pedagogy class that was not confused by the lectures or book chapters on it. I now know I was mistaken. My mistake came from not having enough of a base-level of understanding in physics to be able to apply these concepts effectively to understanding my own vocal training, and to not get confused a year or two down the road. There is a huge interaction between the physiology of the voice and how the physics of vocal resonance, as well as the physics of air pressure to breath support, work. Those connections were simply missing from my pedagogy classes, and, from what I can gather from other conversations with singers, I think it's missing from many singers' academic training as well.
I had such simple misconceptions that I would be embarrassed to admit to in front of anyone with basic physics knowledge, now that I know better. I see a lot of musicians saying some of these same misconceptions quite frequently, and I really, really want us to stop sounding like complete fools in regards to basic math and basic physics to a large portion of the general population (and not just those in hard sciences, either). And I know a lot of singers who would really, really like to not sound like fools, but it's just never been explained well enough, or thoroughly enough, to avoid it. Even if your interest in this might just be cursory, a more thorough understanding of the physics-physiology connection really does help to understand the science behind how the voice, and operatic singing, works and how to apply that knowledge to long-term training.
So here's how this series is going to work: I'm not going to get all up in calculus, cause I'm not interested in making this a math course, but I will present some basic algebraic equations. I will also thoroughly explain these equations so that you can see how the equation is a working representation of how your vocal tract shapes sound. We'll start with the basics and move up from there, but I'm also going to do my best to detail the interaction between physics and physiology...even if I can't get to that interaction until I get a little further down the series. If you've ever been confused looking at a spectrogram of your singing, like in PRAAT, then this series should help you out a lot. It shouldn't be as long as the anatomy and physiology series, so I hope you can hang in here with me. And ultimately, just like the A&P series, I want this to be a reference tool for singers and teachers to be used whenever you need it.
Now, I don't mean to generalize, but I do know a lot of singers who roll their eyes at words like "physics" and "math." In fact, I have had so, so many conversations with musicians about these topics now that I'm taking math and physics courses. They usually go something like this: "I can't meet then because my physics class is at that time. Can you do Monday?" "Physics? Why on Earth are you taking Physics?" "Well, I want to have more detailed knowledge of how the physics of sound and air pressures work so I can understand certain areas of SLP research better." "Well, good for you. I know I would never take those classes. My brain just doesn't work that way." It is that last sentence that I take the most issue with. Why, oh why do we as musicians have to demean ourselves when it comes to the potential our brains have to understand something? Do we even realize the message we're sending out? I mean, we are the people who learn multiple languages for our roles, we learn some anatomy and physiology of the voice, and we are supposed to have at least some foundational knowledge in harmonics and formants when it comes to resonance. This is all in addition to music theory, history, performance practice, etc. Why do we pass off math and physics like it's "over our heads?" Or maybe we want the world to recognize that we're plenty smart in our own right and should be respected for that (which is true). Maybe we think that in order for our field to be respected as art we have to separate so thoroughly from science that we must turn our noses up at it. Maybe we're sick of people in the sciences turning their noses up at us...(I know I'm sick of that). Maybe we don't want to have to add more stuff to our already extensive list of stuff to know. Either way, I do wish my fellow musicians would stop looking at me like I've grown a second head when I say I'm enjoying learning calculus and calculus-based physics. But I digress...
Perhaps most of the issues with math and physics for singers, or just most people in general, comes from the fact that these subjects are very rarely taught well in high school (in the US,) and even in college, for that matter. Much of the time, teachers in these subjects see the class as some sort of grand IQ test in which student's successes or failures have no bearing on the teacher's ability, or inability, to effectively teach the material. That's a common fallacy of certain hard-science classes. (Personally, I liked my calculus's professors take on it: Success in her class, as far as she was concerned, was totally up to the student's dedication and motivation to keep up with the homework (practice) and get help when needed.) So we've relegated the teaching of these concepts to a month or so during a vocal pedagogy class. But maybe, just maybe, voice teachers trying to teach these concepts don't quite give the right amount of time or clarity to these concepts either. I mean, if you're knowledge doesn't have a strong foundation, it is really easy to get confused when, a few years after your pedagogy class, you've been swamped with new information, new ideas, new research, new teachers, new coaches, etc. I know I did!
I thought I got plenty of this stuff in my vocal ped. courses. I thought I had a very good understanding of harmonics, resonance, formants, etc. because I was one of the few in my pedagogy class that was not confused by the lectures or book chapters on it. I now know I was mistaken. My mistake came from not having enough of a base-level of understanding in physics to be able to apply these concepts effectively to understanding my own vocal training, and to not get confused a year or two down the road. There is a huge interaction between the physiology of the voice and how the physics of vocal resonance, as well as the physics of air pressure to breath support, work. Those connections were simply missing from my pedagogy classes, and, from what I can gather from other conversations with singers, I think it's missing from many singers' academic training as well.
I had such simple misconceptions that I would be embarrassed to admit to in front of anyone with basic physics knowledge, now that I know better. I see a lot of musicians saying some of these same misconceptions quite frequently, and I really, really want us to stop sounding like complete fools in regards to basic math and basic physics to a large portion of the general population (and not just those in hard sciences, either). And I know a lot of singers who would really, really like to not sound like fools, but it's just never been explained well enough, or thoroughly enough, to avoid it. Even if your interest in this might just be cursory, a more thorough understanding of the physics-physiology connection really does help to understand the science behind how the voice, and operatic singing, works and how to apply that knowledge to long-term training.
So here's how this series is going to work: I'm not going to get all up in calculus, cause I'm not interested in making this a math course, but I will present some basic algebraic equations. I will also thoroughly explain these equations so that you can see how the equation is a working representation of how your vocal tract shapes sound. We'll start with the basics and move up from there, but I'm also going to do my best to detail the interaction between physics and physiology...even if I can't get to that interaction until I get a little further down the series. If you've ever been confused looking at a spectrogram of your singing, like in PRAAT, then this series should help you out a lot. It shouldn't be as long as the anatomy and physiology series, so I hope you can hang in here with me. And ultimately, just like the A&P series, I want this to be a reference tool for singers and teachers to be used whenever you need it.
Tuesday, January 10, 2012
Sensation vs. Perception: The crux of pedagogical contradictions
Just like Martin Luther King, Jr.,* I have a dream that one day vocal pedagogs will have field-specific, unified terminology that will eliminate the pedagogical confusion so many students experience when moving from one teacher to the next. However, I'm starting to think this dream is too lofty. In the subjective field of vocal training, trying to unify the centuries of pedagaogical terminology with the current science of voice might be a little too much of a hurdle to overcome. I mean, motivated voice students will still desire to read and understand the writings of Lamperti, Garcia, etc. in the context of current voice training, so a complete shift toward unification might alienate the past writings of great pedagogs.
So what are we new pedagogs/voice students supposed to do? How are we supposed to wade through the old information and understand it in terms of the new? I think one piece of the puzzle might be to understand the differences between perception and sensation.
I touched a bit on this near the end of my previous post where I talk about what I feel is happening when I am singing, but it is something I've incorporated into my teaching that, I think, many of my students, even the teenagers, seem to appreciate. One of my high school students had one of her choir teachers give her a few "vocal tips" that seemed to confuse her in terms of what we had been working on in her lesson. Using this established difference between sensation and perception, I was able to explain rather quickly to this student that we were, in fact, working on those things, we were just calling it something different in our lessons. This difference has become such an easy way for my students to begin developing a "tranlation" ability, which I find so, so important, since I know for most of them, I will not be their only voice teacher throughout their training.
What is sensation and what is perception? Sensation is a term used in psychology, as well as anatomy and physiology, to refer to sensory information from the outside world coming into our bodies via the nervous system. When this information reaches your brain, it processes this information, associates it with memories, etc. through some cognitive processing, and then decides how to act. This is the process of perception, which happens to be a very individual process. So sensation (diff. link) is the incoming information, and perception is the interpretation of that incoming information. This works all the time for all of us in some obvious ways: If two friends go to see the same movie, both people receive the same incoming information, i.e. the movie, but they might interpret the "take home message" of the movie in two different ways via their individual perceptions. (How many of us have sent friends articles, etc. where the friend seemed to miss what was, to us, the vital underlying point of the article? You can now blame their perception for getting it wrong...or yours, if you're humble like that.)
How does this work for pedagogy? Well, a lot of the differences we encounter in pedagogical terms comes from the vast differences in the perception of proper singing...at least as far as I perceive it. (Yikes! This article could quickly become an exercise in circular logic, couldn't it?) For example: So much debate has been waged over the "low larynx" issue. Student 1: My teacher said my larynx should never move while singing. Is this right? Student 2: Well, my teacher said research has shown that it does move quite a lot and should raise on high notes, so I guess you're teacher is wrong. Student 1: But my teacher said historical documents all talk about the importance of a lowered larynx, so are all those singers of the past wrong? And the debate rages on. So what's going on here? How can science point to the opposite of what all the great singers and past teachers say they're doing? Sensation and perception! Biologically, the larynx is certainly moving around during singing, and yes, it is raising on high notes. It's a physics-thing that simply must happen. However, when laryngeal efficiency has been obtained, the singer feels like their larynx isn't moving at all and the teacher might not see the larynx raising as much in the throat as it used to. So the singer might perceive that their larynx is stable, but it's just due to how their brain interprets the sensation of laryngeal efficiency throughout their range.
Another example: #1: The ribcage must stay elevated and stable! #2: The ribcage collapses during exhalation out of necessity since the lungs are getting smaller! #1: You're wrong! Here's a youtube video. #2: No, you're wrong! Here's an article by "Prominent Scientist." How does sensation and perception help explain this one? Well, the fact that the chest cavity decreases in size during any exhalation can not be argued. It's another physics-thing that simply must occur. But why would so many singers swear up and down that their rib cage is as stable as stable can be and always elevated during singing? Sensation and perception! The act of using excess muscular effort to keep the rib cage from lowering too fast sends very different sensation information to the brain than what it's used to. For most people, the brain interprets this information with the perception that the rib cage is not moving at all, perhaps because the information is so opposite of what the brain is usually getting about the movement of the rib cage. So you end up with a lot of singers and teachers swearing up and down that the rib cage must not move, when in fact, it must move, but it must move so much more slowly than usual that it feels like it's not moving at all.
I'm sure there are other examples out there, but I cannot think of any at the moment. If you have had a similar debate about another important pedagogical concept, please let me know. I'll see if I can answer it using this sensation/perception model of explanation for ya!
*Disclaimer: This is a dry-humor joke equating my tiny, little dream of unified pedagogical terms to the great deeds accomplished by Dr. King during his lifetime. I'm pretty much an ant on the mountain of his greatness as far as I'm concerned. I've just been watching too many 30 Rock reruns to resist the joke. **
**Disclaimer for the disclaimer: I find dry-humor doesn't always come across online so I felt the need for disclaimer #1. However, upon reading the over-explanation of the joke in disclaimer #1, I realize the already bad original joke has now been effectively destroyed. Awesome.
So what are we new pedagogs/voice students supposed to do? How are we supposed to wade through the old information and understand it in terms of the new? I think one piece of the puzzle might be to understand the differences between perception and sensation.
I touched a bit on this near the end of my previous post where I talk about what I feel is happening when I am singing, but it is something I've incorporated into my teaching that, I think, many of my students, even the teenagers, seem to appreciate. One of my high school students had one of her choir teachers give her a few "vocal tips" that seemed to confuse her in terms of what we had been working on in her lesson. Using this established difference between sensation and perception, I was able to explain rather quickly to this student that we were, in fact, working on those things, we were just calling it something different in our lessons. This difference has become such an easy way for my students to begin developing a "tranlation" ability, which I find so, so important, since I know for most of them, I will not be their only voice teacher throughout their training.
What is sensation and what is perception? Sensation is a term used in psychology, as well as anatomy and physiology, to refer to sensory information from the outside world coming into our bodies via the nervous system. When this information reaches your brain, it processes this information, associates it with memories, etc. through some cognitive processing, and then decides how to act. This is the process of perception, which happens to be a very individual process. So sensation (diff. link) is the incoming information, and perception is the interpretation of that incoming information. This works all the time for all of us in some obvious ways: If two friends go to see the same movie, both people receive the same incoming information, i.e. the movie, but they might interpret the "take home message" of the movie in two different ways via their individual perceptions. (How many of us have sent friends articles, etc. where the friend seemed to miss what was, to us, the vital underlying point of the article? You can now blame their perception for getting it wrong...or yours, if you're humble like that.)
How does this work for pedagogy? Well, a lot of the differences we encounter in pedagogical terms comes from the vast differences in the perception of proper singing...at least as far as I perceive it. (Yikes! This article could quickly become an exercise in circular logic, couldn't it?) For example: So much debate has been waged over the "low larynx" issue. Student 1: My teacher said my larynx should never move while singing. Is this right? Student 2: Well, my teacher said research has shown that it does move quite a lot and should raise on high notes, so I guess you're teacher is wrong. Student 1: But my teacher said historical documents all talk about the importance of a lowered larynx, so are all those singers of the past wrong? And the debate rages on. So what's going on here? How can science point to the opposite of what all the great singers and past teachers say they're doing? Sensation and perception! Biologically, the larynx is certainly moving around during singing, and yes, it is raising on high notes. It's a physics-thing that simply must happen. However, when laryngeal efficiency has been obtained, the singer feels like their larynx isn't moving at all and the teacher might not see the larynx raising as much in the throat as it used to. So the singer might perceive that their larynx is stable, but it's just due to how their brain interprets the sensation of laryngeal efficiency throughout their range.
Another example: #1: The ribcage must stay elevated and stable! #2: The ribcage collapses during exhalation out of necessity since the lungs are getting smaller! #1: You're wrong! Here's a youtube video. #2: No, you're wrong! Here's an article by "Prominent Scientist." How does sensation and perception help explain this one? Well, the fact that the chest cavity decreases in size during any exhalation can not be argued. It's another physics-thing that simply must occur. But why would so many singers swear up and down that their rib cage is as stable as stable can be and always elevated during singing? Sensation and perception! The act of using excess muscular effort to keep the rib cage from lowering too fast sends very different sensation information to the brain than what it's used to. For most people, the brain interprets this information with the perception that the rib cage is not moving at all, perhaps because the information is so opposite of what the brain is usually getting about the movement of the rib cage. So you end up with a lot of singers and teachers swearing up and down that the rib cage must not move, when in fact, it must move, but it must move so much more slowly than usual that it feels like it's not moving at all.
I'm sure there are other examples out there, but I cannot think of any at the moment. If you have had a similar debate about another important pedagogical concept, please let me know. I'll see if I can answer it using this sensation/perception model of explanation for ya!
*Disclaimer: This is a dry-humor joke equating my tiny, little dream of unified pedagogical terms to the great deeds accomplished by Dr. King during his lifetime. I'm pretty much an ant on the mountain of his greatness as far as I'm concerned. I've just been watching too many 30 Rock reruns to resist the joke. **
**Disclaimer for the disclaimer: I find dry-humor doesn't always come across online so I felt the need for disclaimer #1. However, upon reading the over-explanation of the joke in disclaimer #1, I realize the already bad original joke has now been effectively destroyed. Awesome.
Subscribe to:
Posts (Atom)
